I am stuck in this problem for some time now :( :(. it will be very helpful if anyone can give me some hint.
problem link : problem
My idea :
lets consider each light individually.
Let p is the probability of selecting the light. this p can be found easily by calculating each dimension of the 3d cube separately.
Now the expectation for a light will be sum over i(1 to k) : p^i * (1-p)^(k-i). (K is the number of turns) Now we only need to add the terms where i is odd as only then the light will be ON.
calculating this for all the bulbs is obviously time out :( :( :( is there any close form? i can't find it :( :( :(











Edit: Fixed the formula for odd k and added the simplified version.
Thank you very much :).
need to expand the terms :D
If I'm not mistaken, there is no need to expand the terms. Its just thinking about the sum as a sum through a Geometric Progression. If we set a0 = (1 - p)k, we have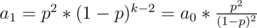 , therefore
, therefore  . It's the same as saying we have a GP with
. It's the same as saying we have a GP with 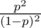 as it's ratio.
as it's ratio.
Now you can just apply basic sum over PG formula to get the end result, using n = ⌊ K / 2⌋, but I couldn't get it right yet
EDIT: I got it right for the test cases now, I was calculating the expected number of turned off lights..
EDIT2: Now that UVa is back, I tested it there, but the simple fact that my solutions uses 2 "pow" calls gives TLE, while with the equation from Jacob I got AC
EDIT3: There are some tricky corner cases for special values of p when using this geometric series approach
I am not sure how you ended up with geometric progression when there must obviously be binomial coefficients somewhere.
That's what I thought in first place, but couldn't go anywhere from this. But I couldn't fix my code with the geometric progression approach either...
Can you explain how you ended up with this formula?
Probability to observe exactly i toggles after k turns for given light is actually Cki·pi·pk - i (binomial distribution).
Now a bit about where my formula came from:
Subtracting one from another you will get:
((1 - p) + p)k - ((1 - p) - p)k = 2·Ck1(1 - p)k - 1p1 + 2·Ck3(1 - p)k - 3p3 + ...