I was working on an interesting problem. (Tip: Homework of algorithm courses can be fun!)
Find the minimum number of (directed) edges to introduce into a directed graph to make it strongly connected (from any vertex you can go to any other vertex). Also, find one configuration of edges to add that satisfies the property and reaches the minimum.
I wonder if this problem is a well-known problem, and if any, what name it is known with? I saw this Stack Overflow question which asks about the minimum number of edges only, not finding one such configuration, and it's said to be "a really classical problem".
I also wonder if there is a more efficient algorithm. My algorithm works in O(V3), which involves several steps to reduce the graph in question into a directed acyclic graph, a weakly connected directed acyclic graph, a connected bipartite graph, and finally giving the answer. A friend says that there is a literature on the internet giving 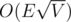 algorithm, but I haven't managed to find it. Or is there an even better algorithm?
algorithm, but I haven't managed to find it. Or is there an even better algorithm?











There was a similar post in Russian half a year ago. You can find paper in English in the comments and my comment in Russian which briefly describes solution (not sure if it's same as in paper).
Hi. Will the answer remain same if the graph if initially disconnected?
I think so.
Divide graph into strongly connected components and you will get a DAG. Number of edges you need to add is a maximum of numbers of vertices with 0 indegree and 0 outdegree (vertices = SCCs). That is a trivial lower bound, but to show that it is sufficient it is significantly harder :P.
For searching the number, it has been given in the Stack Overflow thread above. Proving it's sufficient is simple; just give any algorithm that works and prove its correctness. Optimizing the algorithm is the hard part.
For the algorithm I described in my comment providing the algorithm was the hard part, optimization from O(N3) to O(N) took only one very simple observation.
Could you show me that observation?
Sure. The cubic solution I've mentioned was about finding the maximal matching between sources and sinks, and then adding some edges.
The observation is that we don't really need "maximal" matching, we only need a "blocking" matching (like in Dinic's algorithm), i.e. one which cannot be extended by adding another disjoint path from a source to a sink. And finding "blocking" matching is significantly easier: you just run DFS while you can.
For that trivial lower bound solution, should we add vertices with 0 degree to both numbers of vertices with 0 indegree and 0 outdegree ?
Well think about it. Would the graph be strongly connected if you only added in-edges to those vertices? Why? What might be the intuition for adding these edges anyway?
There is a question which exactly asks this. https://codeforces.com/contest/22/problem/E
Thank you. It's exactly same concept.
Problem https://codeforces.com/gym/103960/problem/H asks exactly that.
I know this is an old post, but I had this question too and it took me some time to find out the answer.
This post is still one of the top google searches for "how to add edges to make a strongly connected graph", so I'm linking to this Stack Overflow article which describes the algorithm for creating the configuration: https://stackoverflow.com/questions/12681785/creating-strongly-connected-components-from-a-dag
I have coded it
Thank you !
Unfortunately the link you provided is now broken, but it can be easily found at the moved repository, i've also added it to my lib, and there is a CSES exercise which asks exactly for it : https://cses.fi/problemset/task/1685
Unrelated but I support how codeforces has the downvote. I hope they never remove it