Is there a way to do this?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 16:01:31 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Yes, there is.
Yes, there is. Think about the formula...
Fi = Fi - 1 + Fi - 2 = 2 * Fi - 2 + Fi - 3 = 3 * Fi - 3 + 2 * Fi - 4....
If you keep on with the formula, assuming F0 = 1 and F1 = 1, you'll reach a point where...
Or, generalizing for every i...
Using those formulas and a recursive function with memoization, you can run the algorithm in no time.
The implementation is very short and simple. Check it out here -> Fibonacci
i can't understand how it works if u call with fib(n+1) it never meet with base case...plz explain
The recursive function doesn't call fib(n+1), it calls fib((n+1) / 2).
ooo sorry i saw wrong,,,that's my eye mistake sorry
That is interesting.
Is this for Fibonacchi Numbers only?
What do you mean? It's a function that calculates the nth Fibonacci number in O(logn).
Generally we do these things by matrix exponentiation.
What I meant to ask is whether it is possible for all such problems to find some formula and solve it. Like you did.
Ahhhhh, I see. I don't know about matrix exponentiation. I always found it very hard and never decided to actually study about it.
I knew Fibonacci numbers could be calculated using matrix exponentiation, but since that's beyond my understanding, I decided to try and find my own method. I did, and I must say I find this method much easier to understand, easier to code and maybe even faster.
I don't know if there's a general formula for other problems that use matrix exponentiation too. I think that there might some that can be solved by a formula and also many others that can't.
If you can formulate your number like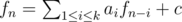 , you can solve it using matrix exponentiation. This is a nice article about it!
, you can solve it using matrix exponentiation. This is a nice article about it!
Thanks for mentioning my blog post! I almost forgot that such post exists :P
Always,when you can present your sequence member using lower grade sequence numbers,you can calculate it in same way,as describe tenshi_kanade
for example: if F(n)=F(n/3)*F(n/3+1)+x you can calculate in O(2^log(3,n))
So we don't actually need matrix exponentiation for such kind of problems? :P
yes,we don't
I instantly thought of Matrix Exponentiation when I read the statement...
But this method is even easier and prettier... m(_ _)m
By the way can anyone say how to calculate Pisano period fast?
There is formulae for prime powers. So you need only factorize modulo.
What formulae?
For p=5^k pisano period is a divisor of 5^k; For p quadratic residue modulo 5 pisano period is a divisor of (p-1)p^{k-1}; For p quadratic nonresidue modulo 5 pisano period is a divisor of 2(p+1)p^{k-1}
i am searching for pisano period (1e9 + 7) any idea?
$$$2e9 + 16$$$
thank you
As zeliboba mentioned above, the Pisano period is a divisor of $$$2(p+1)$$$, since $$$p=10^9+7$$$ is not a quadratic residue modulo $$$5$$$. Then, you can use standard algorithms for finding a multiplicative order of a number. Specifically, to check if the period is a divisor of $$$k$$$, you check that $$$F_k=F_0$$$ and $$$F_{k+1} = F_1$$$.
I'm not sure about this, but you may test it. The formula for the n-th Fibonacci number is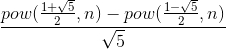
If we write the
powfunction to be fast modulo exponentiation this gives usO(logN)complexity.UPD: This function might not work with double arguments, so this is hardly a right solution.
This formula is applicable iff 5 is a quadratic residue modulo p and p is prime. We can check it using Euler's criterion.
For example, let's take p = 109 + 9. Euler's criterion is true: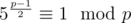 . That means we can find a square root of 5 modulo p.
. That means we can find a square root of 5 modulo p.
Let's find it. I prefer Wolfram Alpha:
powermod[5,1/2,10^9+9] = 383008016. We can insert this number into your formula, and the final result isFn = 276601605·(691504013n - 308495997n)
So this actually works?
Still can't understand where did you get all the numbers in the formula.
They do this by finding some number x such that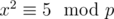 . This is like the
. This is like the  in
in 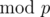 . It turns out that for p = 109 + 9, this x actually exists and is x = 383008016, which you can find out using Wolfram Alpha. They then substitute 383008016 for
. It turns out that for p = 109 + 9, this x actually exists and is x = 383008016, which you can find out using Wolfram Alpha. They then substitute 383008016 for  in your formula and simplify to get those numbers.
in your formula and simplify to get those numbers.
If I am not mistaken, you can do same thing for all modules not equal to 5 by adding roots of x2 - 5 to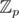 if 5 is not quadratic residue
if 5 is not quadratic residue 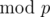 . I mean, calculate value of the same formula on numbers of type a + bx, where
. I mean, calculate value of the same formula on numbers of type a + bx, where 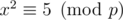 and with rules of addition and multiplication similar to complex numbers (result will always be free of "imaginary" part):
and with rules of addition and multiplication similar to complex numbers (result will always be free of "imaginary" part):
I guess you are right. The thing is the expression never contains square root of five. So we don't really care whether it even exists. It is nice if it does, but it is totally unnecessary. For example my program (link) can calculate Fibonacci numbers modulo 3^6*7^2=35721. And there is no x such that x*x=5 mod 35721. The trick is to work with numbers, similar to complex, with only one difference that i*i=5, not -1.
Nevertheless you can actually use this formula to calculate Fibonacci numbers modulo any odd number. You just need to calculate it not with the help of doubles, but numbers of the form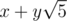 . They have properties similar to complex numbers. For example the product of two numbers
. They have properties similar to complex numbers. For example the product of two numbers  equals
equals 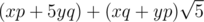 .
.
And because of special structure of this formula, the answer is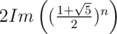 , where Im takes the part right next to square root of five (I called it so because of similarity with complex numbers). So you only need to be able to divide by two and that can be done modulo any odd number.
, where Im takes the part right next to square root of five (I called it so because of similarity with complex numbers). So you only need to be able to divide by two and that can be done modulo any odd number.
Matrix exponentiation
Yes. See this page.
You came and gave a problem: Calculate Fib(n)=Fib(n-1)+Fib(n-2) % M in O(logN). Cool.
Now I come and give you a challenge: SuperFib(n)=A*SuperFib(n-1)+B*SuperFib(n-2)+C*SuperFib(n-3) % M (SuperFib(0), SF(1), SF(2) are given, as well as A, B and C). Solve it in O(logN) time. This requires matrix exponential. If you want to learn something great.
can you link some article related to matrix exponentiation?
Google it yourself.
You could use matrix multiplication here, to get to the Nth number in log(N) time. Here is a video tutorial explaining the same: Fibonacci Numbers using Matrix Multiplication
This is a 2 year old post. Idiot
be polite :(
.
.
.
But he went to GM
.
idk