There's always a problem to fall asleep after a late night (early morning) match, also drinking coffee during competition doesn't exactly help with that. So, here comes a rough write-up of div1 problems.
250 — MissingLCM
As one can verify easily using prime factorization theorem, the LCM of a set of numbers is  , where αp is the maximal power of p which divides some element of the set. Let us find largest pt ≤ n for every prime p ≤ n; there should be a number in [n + 1;m] that divides pt as well. Thus,
, where αp is the maximal power of p which divides some element of the set. Let us find largest pt ≤ n for every prime p ≤ n; there should be a number in [n + 1;m] that divides pt as well. Thus, 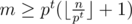 ; there is a case when the new number divides some greater power of p, but we're fine with that. Find the greatest lower constraint for all p ≤ n. Use the Eratosphene's sieve to find all the primes. An O(n) solution is possible.
; there is a case when the new number divides some greater power of p, but we're fine with that. Find the greatest lower constraint for all p ≤ n. Use the Eratosphene's sieve to find all the primes. An O(n) solution is possible.
450 — ColorfulLineGraphs
Consider vertices from left to right. How many ways there are to place a new vertex along with an outcoming edge (if any)? There are k ways to place the vertex without an edge; if we choose the incoming vertex for the new edge, this excludes one color among possible options. Thus, if x vertices were already placed, there are exactly k + x(k - 1) ways to place a new vertex, possibly with an edge. The answer is simply the product k·(k + (k - 1))·(k + 2(k - 1))·.... It suffices to notices that M is rather small, and the product elements are looped modulo M, thus it is easy to find out how many times an element contributes to the product. Take care not to overflow int64. An  solution is possible.
solution is possible.
1000 — BridgeBuilding
Connecting two vertices with a zero-weight edge is effectively the same as merging the vertices into one; we will further go with this interpretation.
Call the parts of the graph between the merged vertices the havens (or whatever); a haven can be a loop or a pair of paths joined together. A loop haven can be represented by a pair of numbers (l, r) — the numbers of merged points in the original enumeration. Denote Ll, r (Rl, r) the largest distance from a vertex of (l, r)-haven to the merged vertex l (r), Sl, r the largest distance between any two vertices of (l, r)-haven, and Dl, r the distance between l and r (after merging each of them). All these numbers can be computed in O(n3) for all pairs (l, r) (use two pointers to compute Sl, r).
Suppose we have chosen pairs of vertices to merge; which pair of vertices can be farthest apart now? The farthest pair of vertices (u, v) can lie in the same haven, or in different havens. In the first case all pairs of vertices will be considered explicitly; in the second case the distance is equal to L + D1 + ... + Dk + R, where L is the distance from u to the closest merged vertex, D1, ..., Dk are distances between consecutive merged vertices inside a single haven, and R is the distance from the last merged vertex to v.
Binary search the diameter x. Compute dpi, j with the following meaning: suppose we merged j pairs of vertices with last pair to merge having index i, we also took care that in the processed part no pair of vertices is at distance larger than x; than dpi, j is the largest value of L + D1 + ... + Dk such that the last merged vertex of Dk is the merged vertex i. Initialize dpi, 1 with the two-paths havens, after that consider all possible options for the next vertex i; consider pairs of points in the current haven using Sl, r and all the rest using the DP value. Finally, to find the answer use such dpi, k that the last two-paths haven does not have its vertices too far apart, and also dpi, k + taili ≤ x, where taili is the largest distance from i to any of the ends. That makes for an  solution, also probably a highly optimized O(n4) might pass.
solution, also probably a highly optimized O(n4) might pass.











for problem 500 of div 2
problem link: http://community.topcoder.com/stat?c=problem_statement&pm=13546
My code: http://ideone.com/C18KQk
what is wrong with my solution ??