Thanks everybody for participating. Tasks follow in the order of the original contest (the mirror order is given in the brackets).
562A - Logistical Questions
(in mirror: 566C - Logistical Questions)
Let's think about formal statement of the problem. We are given a tricky definition of a distance on the tre: ρ(a, b) = dist(a, b)1.5. Each vertex has its weight wi. We need to choose a place x for a competition such that the sum of distances from all vertices of the tree with their weights is minimum possible: f(x) = w1ρ(1, x) + w2ρ(x, 2) + ... + wnρ(x, n).
Let's understand how function f(x) works. Allow yourself to put point x not only in vertices of the tree, but also in any point inside each edge by naturally expanding the distance definition (for example, the middle of the edge of length 4 km is located 2 km from both ends of this edge).
Fact 1. For any path 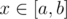 in the tree the function ρ(i, x) is convex. Actually, the function dist(i, x) plot on each path [a, b] looks like the plot of a function abs(x): it first decreases linearly to the minimum: the closes to i point on a segment [a, b], and then increases linearly. Taking a composition with a convex increasing function t1.5, as we can see, we get the convex function on any path in the tree. Here by function on the path we understand usual function of a real variable x that is identified with its location on path x: dist(a, x). So, each of the summands in the definition of f(x) is convex on any path in the tree, so f(x) is also convex on any path in the tree.
in the tree the function ρ(i, x) is convex. Actually, the function dist(i, x) plot on each path [a, b] looks like the plot of a function abs(x): it first decreases linearly to the minimum: the closes to i point on a segment [a, b], and then increases linearly. Taking a composition with a convex increasing function t1.5, as we can see, we get the convex function on any path in the tree. Here by function on the path we understand usual function of a real variable x that is identified with its location on path x: dist(a, x). So, each of the summands in the definition of f(x) is convex on any path in the tree, so f(x) is also convex on any path in the tree.
Let's call convex functions on any path in the tree convex on tree. Let's formulate few facts about convex functions on trees.
Fact 2. A convex function on tree can't have two different local minimums. Indeed, otherwise the path between those minimums contradicts the property of being convex on any path in the tree.
So, any convex function f(x) on the tree has the only local minimum that coincides with its global minimum.
Fact 3. From each vertex v there exists no more than one edge in which direction the function f decreases. Indeed, otherwise the path connecting two edges of function decrease would contradict the definition of a convex function in a point v.
Let's call such edge that function decreases along this edge to be a gradient of function f in point x. By using facts 2 and 3 we see that in each vertex there is either a uniquely defined gradient or the vertex is a global minimum.
Suppose we are able to efficiently find a gradient direction by using some algorithm for a given vertex v. If our tree was a bamboo then the task would be a usual convex function minimization that is efficiently solved by a binary search, i. e. dichotomy. We need some equivalent of a dichotomy for a tree. What is it?
Let's use centroid decmoposition! Indeed, let's take a tree center (i. e. such vertex that sizes of all its subtrees are no larger than n / 2). By using fact 3 we may consider the gradient of f in the center of the tree. First of all, there may be no gradient in this point meaning that we already found an optimum. Otherwise we know that global minimum is located in a subtree in direction of gradient, so all remaining subtrees and the center can be excluded from our consideration. So, by running one gradient calculation we reduced the number of vertices in a considered part of a tree twice.
So, in  runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them.
runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them.
Now let's calculate the gradient direction in a vertex v. Fix a subtree ui of a vertex v. Consider a derivative of all summands from that subtree when we move into that subtree. Denote this derivative as deri. Then, as we can see, the derivative of f(x) while moving from x = v in direction of subtree ui is - der1 - der2 - ... - deri - 1 + deri - deri + 1 - ... - derk where k is a degree of vertex v. So, by running one DFS from vertex v we may calculate all values deri, and so we may find a gradient direction by applying the formula above and considering a direction with negative derivative.
Finally, we got a solution in  .
.
562B - Clique in the Divisibility Graph
(in mirror: 566F - Clique in the Divisibility Graph)
Order numbers in the sought clique in ascending order. Note that set X = {x1, ..., xk} is a clique iff  for (1 ≤ i ≤ k - 1). So, it's easy to formulate a dynamic programming problem: D[x] is equal to the length of a longest suitable increasing subsequence ending in a number x. The calculation formula:
for (1 ≤ i ≤ k - 1). So, it's easy to formulate a dynamic programming problem: D[x] is equal to the length of a longest suitable increasing subsequence ending in a number x. The calculation formula: 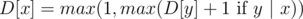 for all x in set A.
for all x in set A.
If DP is written in "forward" direction then it's easy to estimate the complexity of a solution. In the worst case we'll process 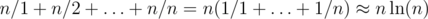 transitions.
transitions.
562C - Restoring Map
(in mirror: 566E - Restoring Map)
Let's call a neighborhood of a vertex — the set consisting of it and all vertices near to it. So, we know the set of all neighborhoods of all vertices in some arbitrary order, and also each neighborhood is shuffled in an arbitrary order.
Let's call the tree vertex to be internal if it is not a tree leaf. Similarly, let's call a tree edge to be internal if it connects two internal vertices. An nice observation is that if two neighborhoods intersect exactly by two elements a and b then a and b have to be connected with an edge, in particular the edge (a, b) is internal. Conversely, any internal edge (a, b) may be represented as an intersection of some two neighborhoods С and D of some two vertices c and d such that there is a path c – a – b – d in the tree. In such manner we may find all internal edges by considering pairwise intersections of all neighborhoods. This can be done in about n3 / 2 operations naively, or in 32 times faster, by using bitsets technique.
Note that knowing all internal edges we may determine all internal vertices except the only case of a star graph (i. e. the graph consisting of a vertex with several other vertices attached to it). The case of a star should be considered separately.
Now we know the set of all leaves, all internal vertices and a tree structure on all internal vertices. The only thing that remained is to determine for each leaf, to what internal vertex is should be attached. This can be done in following manner. Consider a leaf l. Consider all neighborhoods containing it. Consider a minimal neighborhood among them; it can be shown that it is exactly the neighborhood L corresponding to a leaf l itself. Consider all internal vertices in L. There can be no less than two of them.
If there are three of them or more then we can uniquely determine to which of them l should be attached — it should be such vertex from them that has a degree inside L larger than 1. If there are exactly two internal vertices in L (let's say, a and b), then determining the attach point for l is a bit harder.
Statement: l should be attached to that vertex among a, b, that has an internal degree exactly 1. Indeed, if l was attached to a vertex with internal degree larger than 1, we would have considered this case before.
If both of vertices a and b have internal degree — 1 then our graph looks like a dumbbell (an edge (a, b) and all remaining vertices attached either to a or to b). Such case should also be considered separately.
The solution for two special cases remains for a reader as an easy exercise.
562D - Restructuring Company
(in mirror: 566D - Restructuring Company)
This problem allows a lot of solution with different time asymptotic. Let's describe a solution in  .
.
Let's first consider a problem with only a queries of second and third type. It can be solved in a following manner. Consider a line consisting of all employees from 1 to n. An observation: any department looks like a contiguous segment of workers. Let's keep those segments in any logarithmic data structure like a balanced binary search tree (std::set or TreeSet). When merging departments from x to y, just extract all segments that are in the range [x, y] and merge them. For answering a query of the third type just check if employees x and y belong to the same segment. In such manner we get a solution of an easier problem in  per query.
per query.
When adding the queries of a first type we in fact allow some segments to correspond to the same department. Let's add a DSU for handling equivalence classes of segments. Now the query of the first type is just using merge inside DSU for departments which x and y belong to. Also for queries of the second type it's important not to forget to call merge from all extracted segments.
So we get a solution in 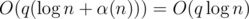 time.
time.
562E - Max and Min
(in mirror: 566G - Max and Min)
Consider a following geometrical interpretation. Both Max and Min have a set of vectors from the first plane quadrant and a point (x, y). During his turn Max may add any of his vectors to a point (x, y), and Min — may subtract any of his vectors. Min wants point (x, y) to be strictly in the third quadrant, Max tries to prevent his from doing it. Denote Max vectors as Mxi and Min vectors as Mnj.
Consider a following obvious sufficient condition for Max to win. Consider some non-negative direction in a plane, i. e. such vector (a, b) that a, b ≥ 0 and at least one of numbers a, b is not a zero. Then if among Max vectors there is such vector Mxi, that it's not shorter than any of Min vectors Mnj along the direction (a, b) then Max can surely win. Here by the length of vector v along a direction (a, b) we mean a scalar product of vector v and vector (a, b).
Indeed, let Max always use that vector Mxi. Then during the turns of Max and Min point (x, y) is shifted by a vector Mxi - Mnj for some j, so its overall shift along the vector (a, b) is equal to ((Mxi - Mnj), (a, b)) = (Mxi, (a, b)) - (Mnj, (a, b)) ≥ 0. By observing that initially the scalar produt ((x, y), (a, b)) = ax + by > 0 we see that at any moment ax + by will be strictly positive. This means that Min won't be able at any moment to make x and y both be negative (since it would mean that ax + by < 0).
Now let's formulate some kind of converse statement. Suppose Max vector Mxi lies strictly inside the triangle formed by Min vectors Mnj and Mnk. In particular, vector Mxi endpoint can't lie on a segment [Mnj, Mnk], but it may be collinear one of vectors Mnj and Mnk.
Note that since Mxi lies strictly inside the triangle formed by vectors Mnj and Mnk it can be extended to a vector Mx'i, whose endpoint lies on a segment [Mnj, Mnk]. By using linear dependence of Mx'i and Mnj, Mnk we have that Mx'i = (p / r)Mnj + (q / r)Mnk, where p + q = r and p, q, r — integer non-negative numbers. This is equivalent to a formula rMx'i = pMnj + qMnk. This means that if per each r turns of Max in Mxi we will respond with p turns of Min in Mnj and q turns of Min in Mnk, then the total shift will be equal to - pMnj - qMnk + rMxi = - rMx'i + rMxi = - r(Mx'i - Mxi), that is the vector with strictly negative components. So, we are able to block that Max turn, i. e. it does not give any advantage to Max.
The natural wish is to create a convex hull of all Min turns and to consider all Max turns in respect to it. If Max turn lies inside the convex hull of Min turns, then by using the previous fact this turn is meaningless to Max. Otherwise, there are two possibilities.
First, this turn may intersect the hull but go out of it somewhere; in this case this Max turn is no shorter than all Min turns in some non-negative direction (more specifically, in its own direction), so Max wins.
On the other hand, Max vector lies to aside from the Min turns convex hull. Let's suppose the vector Mxi lies to the left of the Min turns. This case requires a special analysis. Consider the topmost of the Min vectors Mnj. If Mxi is no lower than Mxj, then by using the first fact Max is able to win by using only this vector. Otherwise the difference Mni - Mxj is a vector with strictly negative components, by using which we are able to block that Max vector.
So, the full version of a criteria for Min being a winner looks like the following. Consider a convex hull of Min turns and expand it to the left of the topmost point and to the bottom of the rightmost point. If all Max turns lie strictly inside the formed figure then Min wins, otherwise Max wins.
562F - Matching Names
(в трансляции: 566A - Matching Names)
Form a trie from all names and pseudonyms. Mark with red all vertices corresponding to names, and with blue all vertices corresponding to the pseudonyms (a single vertex may be marked several times, possibly with different colors). Note that if we match a name a and a pseudonym b, then the quality of such match is lcp(a, b) = 1 / 2(2 * lcp(a, b)) = 1 / 2(|a| + |b| - (|a| - lcp(a, b)) - (|b| - lcp(a, b))), that is equal to a constant 1 / 2(|a| + |b|), with subtracted half of a length of a path between a and b over the trie. So, what we need is to connect all red vertices with blue vertices with paths of a minimum possible total length.
This can be done with a following greedy procedure: if we have a vertex v with x red vertices and y blue vertices in its subtree then we must match min(x, y) red vertices of its subtree to min(x, y) blue vertices of its subtree and leave the remaining max(x, y) - min(x, y) ref or blue vertices to the level higher. The correctness of such algorithm may be easily shown by the next idea. Give each edge of each path a direction from a red vertex to a blue. If some edge recieves two different directions after this procedure, we may cross-change two paths through it so that their total length is reduced by two.
So, we get a solution in O(sumlen) where sumlen is a total length of all names and pseudonyms.
562G - Replicating Processes
(в трансляции: 566B - Replicating Processes)
==== UNTRANSLATED SECTION, PLEASE WAIT A FEW MINUTES... ====

Kitten to take your attention :)
This problem may be solved by simulating the replication process. Let's keep a list of all replications that may be applied by the current step. Apply an arbitrary replication, after that update a list by adding/removing all suitable or now unsuitable replications touching all affected on current step servers. The list of replications may be kept in a "double-linked list" data structure, that allows to add and remove elements to/from the set and to extract an arbitrary element of the set in O(1).
The proof of correctness of such algorithm is not hard and is left as an exercies (maybe it will appear here later).
We got a solution in O(n) operation (though, the constant hidden by O-notation is pretty large; the input size is already 12n numbers and the solution itself hides a constant 36 or higher).














When you realize that problem Max and Min is a convex hull problem
For problem D — Restructuring Company the first solution coming to my mind was to use a Segment Tree supporting these operations:
Then create the tree of size N and for the operations:
This can be done with some kind of lazy propagation but I'm not sure if fits in the time limit.
P.S: I didn't take part in contest but I read this problem, I'll try to implement this solution when I have the time.
Maybe I didn't get get your idea right, but I don't think it is going to work.
Try it on second sample. You have
1 2 3 4 5 6 7 8
at the beginning.
After first merge it becomes
1 2 3 4 2 6 7 8
Now second merge comes. If you are going to implement it in the way you described, your array will become:
1 2 3 4 4 4 4 8.
You have already lost information about 2 and 5 being in a same component — you repainted 5 with 4 after last query, but 2 remains painted with 2 (instead of being changed to 4 to remain same as 5).
Oh, you are right, I'm not sure if can be made some tricks to make it work but surely is overkill comparing with editorial solution.
Thanks, I only read the problem before going to take the lunch and build this idea while walking, never tried in paper or sample cases but I liked the problem.
What if we first query the range for the minimum value present(say x), and then update the range to x?
So here after second merge our answer will become(as minimum value is 2)
1 2 3 2 2 2 2 8
Now move to the next part of sample 2 and merge 1 with 2 :)
Now it is definitely an overkill. :P
for this part I thought about another infromation for every node called
bestwhere the best value for some range is the smallest parent of all elements parents and I'll propagate this information upward.
So for the sample input, the node with range [4,7] will have have it's best value equal to
2.Will this work ??
My idea has a little bit different to k790alex, I use DSU + Segment Tree(Lazy), when
I merge x and y the result is min of them. I using update to merge x,x+1,..y but when using DSU I can control the parent of them. I think it so perfect but it is wrong answer on test 3. My submission: 222029107
I'm not good at English, but I tried explain my idea, I want to contact to everybody. I'm sorry about that
It can be done with segment tree and DSU. No need for lazy propagation. Just keep array of visited nodes, so when you update an interval, you dont need to worry if some nodes below visited ones are already in the same group. Code.
Problem D, I use another method and passed all tests. And the time complexity seems to be . Usa a array to mark the next index which elements is not in the same union, to deal with second type of query. So in the second type of query, every elements will just be merge once, so it is linear. 12278498
. Usa a array to mark the next index which elements is not in the same union, to deal with second type of query. So in the second type of query, every elements will just be merge once, so it is linear. 12278498
Ignore.
I tried simulating in Problem G — Replicating Processes but it is giving me WA. If you kept applying any arbitrary move that is possible as said in the editorial, we will fail sample test 1 itself.
An arbitrary order of valid moves in sample test 1 can look like this —
1 2 5 6 7 3
And this results in the final configuration being 7 processes for server 1 and 7 processes for server thus giving us a deadlock. So there is obviously something I am missing :/
Can someone please elaborate?
up to 9 processes at a single time, so both remaining operations are valid ( no deadlock ) ...
Ohh yeah missed that :P
So how do you prove this strategy then?Solved.
Why is it always possible to find a valid sequence of execution? I am unable to prove it. From what I could get from the editorial, given a sequence of steps we have already done, it is always possible to find a new rule which will be valid. Why is it so?
This is what I believe is the "proof" and it was enough to convince me.
Each server initially has 4 processes and each process will be replicated. Consider first the case where each replication is of the form A -> A, A. It is easy to see that in this case all replications can be carried out directly.
Now consider the case where we change one replication of the form A -> A, A to A -> A, B. This replication can also be carried out and now server B has 9 processes in its memory. But we know that in the final configuration, each server should contain exactly 8 processes in its memory. This means that one replication in B will change from B -> B, B to B -> B, X.
This will produce a chain reaction until we form a cycle. It is in fact guaranteed that a cycle will form since currently, server A has only 7 processes in its memory and it needs 8 so eventually we will get a cycle. Thus we can perform the replication by starting at any point in this cycle and finish the replication process. This argument can be extended to replications of the form A -> X, Y. Thus it is always possible to perform all the replication requests.
thanks for Editorial ;)
You'r welcome ;)
Are you Zlobober ?!! ;))
I have implemented algorithm mentioned in editorial for problem 'F. Clique in the Divisibility Graph' in Python which is getting TLE. But the same solution is accepted in Java. Is algorithm mentioned in editorial not applicable for Python?
Please find the link to find my submissions. Python: 12295295 Java: 12295231
Thanks in advance.
Accepted with Pypy. Typically, Python is slower than C++, and Pypy is faster than Python.
Thanks ItsLastDay. But does codeforces have different time limits for different programming languages like codechef?
As far as I know, on Codeforces time limits are the same for different languages.
In "Clique in the Divisibility Graph",what is meant by "xi | xi+1"?
| means "divides", so x_{i+1} is a multiple of x_i.
Thanks for the editorial.
I don't understand something about solution of problem Logistical Question. Why do we use derivatives to find gradient direction? How can we get the formular of these derivatives?
Thanks.
It's well-known that function decreases if its derivative is negative. We don't have a derivative of a function in a point that is vertex of the tree in normal sence, but we have a one-sided derivative of its value when we move along some edge. Let's denote this derivative as .
.
Let's express value of f(x) as s1(x) + ... + sk(x) where s1, ..., sk are summands that are taken from each of the k subtrees of vertex v. Then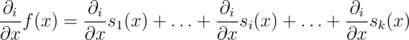 .
.
Let's denote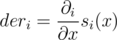 . Then it's easy to see that
. Then it's easy to see that  for j ≠ i (if when we move along the edge, the function decreases with some speed, then when we move to the other edge in the opposite direction, it will increase with the same speed). So, we get the formula from the editorial:
for j ≠ i (if when we move along the edge, the function decreases with some speed, then when we move to the other edge in the opposite direction, it will increase with the same speed). So, we get the formula from the editorial:  .
.
Thanks for your nice explaination. I got it now.
An alternative solution to problem 566E:
Define F(u, v) as the number of neighborhoods that contain both vertex u and vertex v. (u != v)
Observation: F(u, v) = 1 if and only if dist(u, v) = 4, F(u, v) = 2 if and only if dist(u, v) = 3 and F(u, v) > 2 if and only if dist(u, v) <= 2. (an exception: n = 2, this time we can simply output "1, 2") Using bitsets, we can easily find all F(u, v)s in O(n^3 / w) time so that we know all pairs of vertices that have a distance 3 or 4, which forms a weighted graph G.
Let the diameter of the tree be D.
D is 2(D can't be 1 for n > 2) if and only if G has no edges. In this situation, we can output any tree of diameter 2.
D is 3 if and only if G has some edge(s) of weight 3 but no edges of weight 4. Then G must be a complete bipartite graph plus 2 isolated vertices. The order of the isolated vertices doesn't matter.
Otherwise:
Let a vertex be black if its distance to 1 is even, and white if it's not black.
D is 4 if and only if G has 1 connected component plus an isolated vertex. The latter vertex must be the center, and its color should be the same as that of the diameter's endpoint.
If D is larger than 4, G is connected and it's easy to determine the color of each vertex.
After coloring each vertex, it's easy to figure out that two vertices u and v are connected if and only if F(u, v) >2 and u and v are in different colors.
Total complexity: O(n^3 / w)
This can also be used to check whether it's possible to satisfy the constraints.