Little Red Riding Hood and Candy Factory
The problem basically asks to check if the integer is even or odd. As integer is very large you can check if last digit is even or odd to decide the ans. If the integer is even than the ans is YES else ans is NO
Little Red Riding Hood and Convolutions
Convolution(L) = L1*L2*L3*L4 + L2*L3*L4*L5 + ........
Since only allowed values for L[i] is 1 or -1, we can say that the number of terms (Li*Lj*Lk*Ll) which evaluates to -1 are equal to number of terms which evaluates to 1. So, if we negate the given list the number of terms which evaluates to -1 or 1 doesn't change and we get another list L' whose Convolution(L') = 0
An Unfair Fair Game
Greedy, O(k):
Lets start with simple greedy solution. Given n, subtract k, k-1, k-2 from n till the residue of number is between 0 to k. If the residue is non-zero, add the remaining number to the answer set, and report (k — the cardinality of the answer set).
Optimizing greedy to just count the cardinality, O(log(k)):
Observe that the numbers we are subtracting form a simple AP, {k, k-1, …, k-x}. The sum of this is S(x): k*(k+1)/2 — (k-x-1)*(k-x)/2. This is a strictly decreasing function in the range x = [1, k]. We can do binary search to find the first non-negative value of S(x). Let this value occur at x = z, answer is (k — (z + (s(z) == 0))).
Expected complexity : O(log(k))
Graph Sum
We have to support two queries, add a value to a vertex and print the subtree sum.
Finding the value:
- if m is odd then no. of ways to form m by 2 and 4 is zero.
- if m is even then no. of ways is equal to the no. of ways of forming m/2(let say R = m/2) by 1 and 2.
which is actually SIGMA(i = 0 to R-1) ((R-i-1) Choose (i)) which is fibonacci number Fib(R)
Taking last 5 digits is nothing but mod operation with 105. Fib(R) repeats after 150000 when we take mod with 105.
Now add the (no. of ways) * m to every vertex in path from v to vertex 1(root). Use HLD to perform the query.
Expected Complexity : O(N*log2(N))
HLD Tutorial : Tutorial
Alternate way to solve the problem : grikukan's solution
Code Land
The problem statement reduces to this:
Given an undirected weighted graph and information of weights of every edge. Remove one bridge and add another such that the weight of the graph is maximized.
Lets see what the brute force solution for this will be. Lets try adding every edge and removing minimum weight bridge corresponding to that edge. The complexity of this solution will be O(n3).
Lets see how we can optimize this code.
Claim 1: Every bridge of the graph will be in ST.
Proof : Let say tree T is a ST of graph but there is an edge e (x, y) which is not in this ST. Now, as e is not in ST than there is no way to go from x to y (By definition of bridge. The bridge is the only way to reach y from x). That means ST is not connected and hence is not ST, Therefore every bridge of the graph has to be in the ST.
Now, we have a ST which contains all the nodes and all the bridges. Lets find the minimum weight bridge between every pair of nodes (n1, n2). Since, now we have a tree there is only one path from any one node to another, we can find this minimum weight bridge between every pair of nodes by doing n dfs.
Now, lets try out our original solution. Since, now we know the minimum weight bridge for every pair of node we can do the same solution in O(n2).
Final running time : O(n2)
Range Query
To solve this problem we will use MO's algorithm. If we have sorted our queries with MO's. We can than use range query and range update data structures to solve the problem. For any add or remove we need to update [A[i] — k, A[i] + K] and correspondingly we will add and subtract cnt of range [A[i] — k, A[i] + k] from our ans.
We need to use BIT rather than Segment tree (I tried with both and there was a huge difference between time taken to generate ans by both codes. I think the reason for this was recursion but not sure. If anyone know the exact reason please comment.).
Expected complexity : O(n*sqrt(n)*log(n))
Sources for MO's algorithm : Tutorial
If you find any issues with the editorials let us know. Thanks for participating. :)











Auto comment: topic has been updated by ashish1610 (previous revision, new revision, compare).
Auto comment: topic has been updated by ashish1610 (previous revision, new revision, compare).
Auto comment: topic has been updated by ashish1610 (previous revision, new revision, compare).
I think in Graph's sum it's easier(and have better complexity) to do this:
1) Build euler tour of tree and for each verticle remember first and last position in tour
2) Add number to verticle = add number to first position of verticle in tour
3) Sum in subtree = sum of segment between first and last position it tour.
2 and 3 can be done using segment tree.
It has complexity O(n + qlogn)
This is a really great idea. Thanks, updated ;)
are these problems going to appear in practise section? if so, then when? thanks.
Search for the problem codes here :)
https://www.codechef.com/problems/extcontest/
fib(n)can also be found inlog(n)with fast exponentiation andnice blog about it
I didn't understand how you got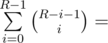 number of ways to make R using 1 and 2 in Graph Sum and how that connects to the R'th Fibonacci number, instead I came up with another approach, which I feel is more intuitive.
number of ways to make R using 1 and 2 in Graph Sum and how that connects to the R'th Fibonacci number, instead I came up with another approach, which I feel is more intuitive.
Number of ways to form R using 1, 2 i.e. ways(R) = ways(R - 1) + ways(R - 2). Since the base case is ways(1) = ways(2) = 1, we can see that this recurrence is the same as that for the Fibonacci numbers.
But I would really like to understand the author's method as well. Can someone please elaborate?
No. of ways to make R:
0 two = (R choose 0) : all 1
1 two = (now we have R-1 no. and 1 among them will be two) = (R-1 choose 1)
2 two = (same way we have now R-2 no. and 2 among them are two) = (R-2 choose 2)
.
.
.
R/2 two = (R/2 choose R/2): all 2
R/2 + 1 two = 0 ways
.
.
R two = 0
this series is diagonal in pascal triangle which sums to FIB(R) (FIB(R+1) if FIB(0) = 1, FIB(1) = 1)
Got it. Thanks! :)