JAG summer 2015 Day4 (= OpenCup GP of Japan) J: Black Company

At first, we define persons A and B are friends each other if they are close to each other or there is a person C s.t. A and B are close to C.

To simplify, we assume all c_i is distinct. Then all salary relationships between two friends must be directed, i.e. we obtain a DAG, which is a subgraph of the total-order graph with respect to c_i's. Here, the salary p_v of a person v must be greater than the salary of all the persons who point to v on the DAG. We want to minimize p_v, hence 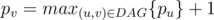must be satisfied. Since the graph is a DAG, optimal p_v for all v can be calculated by dynamic programming according to its topological order (with initializing 0-in-degree vertices to 1). If the DAG has E edges, this algorithm is O(N + E).

But how large is E? If we calculate all the friend relations naively, E = O(N²) in the worst case (e.g. star graph). We can avoid such situation by storing persons at vertex v who are (directly) close to v. Then we sort these persons with respect to c_i's, and connect only adjacent persons in the sorted list. It is sufficient because the friend relations between persons in the list are total-order, and this total-order is well-represented by a single linear extension. The sum of the number of persons stored at each vertex is 2M, this pre-computation takes only O(MlogM) time, and E = O(M).

Finally, we should think of the case in which there are persons who have the same c_i. In this case, we can consider as these persons are equivalent (note that c_i < c_j iff p_i < p_j imply p_i = p_j if c_i = c_j), so we merge vertices representing them. We note that the output is the sum of 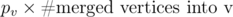. We can use Union-Find tree, strongly connected component decomposition, or something in order to merge, and these take about O(M) time.

In conclusion, we can solve this problem in O(MlogM) time.