I want to compute sum of maximum of all sub arrays in O(n)
till now i came up with an O(n^2) algo.
for better explanation of the problem, I want to reduce the complexity of this one liner.
print sum(max(arr[i:j]) for i, j in combinations(xrange(len(arr)), 2))
also assume that the array may contain equal elements.
Sample Test:
Input:
5
1 2 1 1 2
Output:
16
please help me.
PS: sorry for this duplicate post, when i'm editing the problem statement, i clicked discard button thinking that it will discard the edits but it deleted the entire post.










Is this normal that for [1] your answer is 0? And answer for your sample equals to 26, I think.
Maybe you mean print sum(max(arr[i:j]) for i, j in combinations(xrange(len(arr) + 1), 2))
A way to solve this problem is using Cartesian tree and a little combinatorics. Here is the code(problem is cf round 333 div2D, after a little trick the problem is degenerated to your problem) Code
The main idea is as follows: First you build the cartesian tree. Then you traverse the tree in DFS. Let the current node be v at position i. We also keep the interval [l, r] for which v is maximum. The total count of all subarrays that include v are (r — i + 1) * (i — l + 1), so for them the maximum is count * arr[v]. Next step is recursive call to the left part of array and right part(e.g [l, i — 1] and [i + 1, r]), with maximums that correspond to left and right children in cartesian tree. Everything is summed and we have the answer.
PS: my solution also counts arrays with length 1. If you want to count only arrays with length >= 2, you must subtract the sum of the array from the result.
There is a much easier O(N) approach:
For each index i, compute these two quantities:
L[i] = largest j such that j < i and A[j] > A[i]
R[i] = smallest j such that j > i and A[j] ≥ A[i]
If we compute these two arrays, we can find out the contribution of each A[i] to the final answer.
This can be done as follows:
Contribution[i] = (i - L[i]) * A[i] * (R[i] - i)
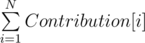
We can precompute L and R in O(N) using stacks.
Ans =
P.S : There might be bugs in the formula, but the idea in general should work.
this does't work if there r equal elements. on test n == 100000
1 1 1 1...
answer is n * (n — 1) / 2.
observe that, A[j] > A[i] for L and A[j] >= A[i] for R
so L and R will look like
Yeah :)