Hello folks,
I have a small doubt regarding Dijkstra Algorithm
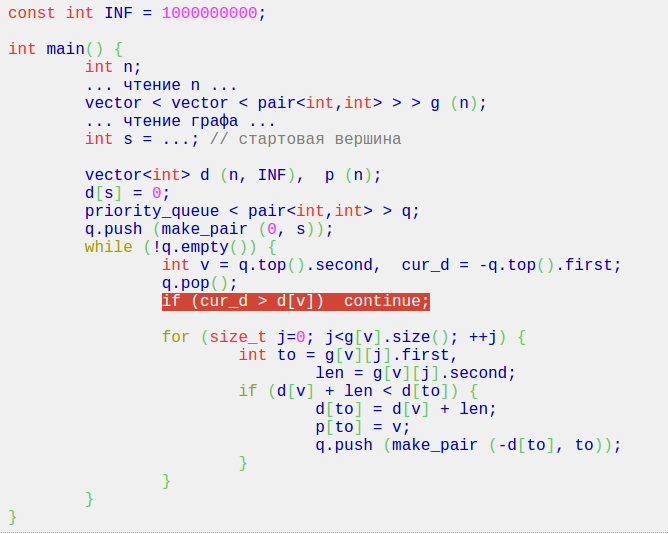
The highlighted part,
What's the main use of the line?
Thanks in Advance and Merry Christmas!| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 7 | SecondThread | 150 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Hello folks,
I have a small doubt regarding Dijkstra Algorithm

The highlighted part,
What's the main use of the line?
Thanks in Advance and Merry Christmas!| Name |
|---|



Same node can be pushed into queue more than once, those same nodes in queue have distinct costs.It is enough to update queue just with the smallest cost value for a node. That "if" make loops work just once for each node.
Ok thanks ,
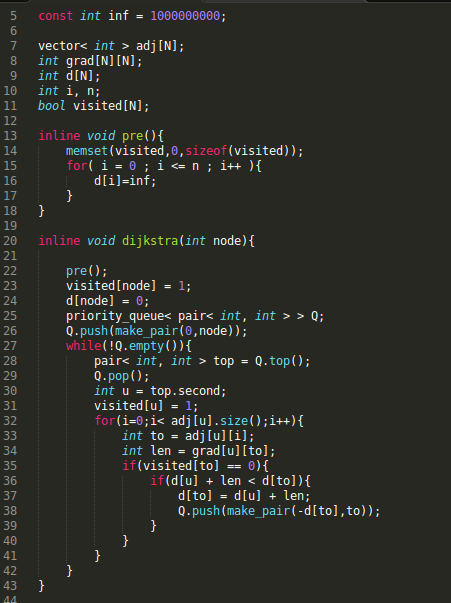
So, does this code work fine instead of using that line ?
It will work, but you'll have a lot of edge visiting because some input can make your code run in O(n^2 log n). For example, if the edge list looks this (n = 10^5, format "u v w"
What's happening here is every node in the range [2: 49999] has an edge from node 1 with a uniform weight of 1. All if them will be visited normally.
However, once the second batch will be processed, all edges from [2: 49999] will converge to node 50000. Note that d[50000] will be updated 49998 times before visiting node 50000 and thus node 50000 will be pushed that number of times in the priority queue before it will be officially visited.
Here comes the hack. Since you are not checking (and breaking) if the visited state has a different min distance, come third wave of edges from 50000 to [50001: 100000] you will end up adding 50000 edges 49998 times. Your algorithm does not fail but it's now O(n^2 log n) instead of O(n log n).
That's just one edge case. The one line
if (cur_d > d[v]) continue;ensures you visit every node once. You can also doif (visited[u]) continue;right before your for loop in your dijkstra version, and that will do the trick.