Hi :)
Some problem about powerful data structure and algorithm SQRT decomposition.
If you want to learn this algorithm click here.
And a big thank to mr_agha_seyed for helping.

220B - Little Elephant and Array
86D - Powerful array
13E - Holes
455D - Serega and Fun
375D - Tree and Queries
446C - DZY Loves Fibonacci Numbers
487D - Conveyor Belts
506D - Mr. Kitayuta's Colorful Graph
348C - Subset Sums
617E - XOR and Favorite Number
444C - DZY Loves Colors
398D - Instant Messanger
342E - Xenia and Tree
Maybe some of them can solve by other data structures like segment tree.











cheers! :) :D
Would be nice to have SQRT decomposition tag for those problems. Now, I guess, all of them in data structures
http://codeforces.com/problemset/tags/data%20structures
It says — Link not found.
The link to problemset with tags got changed when ratings to problems were included. The previous link just means adding data-structures as a tag to problemset. So, here's the new link: https://codeforces.com/problemset?tags=data%20structures
Thank You. I'll try them all O_o
timus 1846 also nice sqrt-decomp problem.
Can you, please, elaborate a bit?
I'm thinking of splitting the queries in chunks of sqrt(N) and processing them similar to the disjoint-set-union split as described on e-maxx.
First of all, we will call a set a DS which can handle the insert and erase operations in O(1).
Let active set and temp. set be 2 empty sets
For every chunk of sqrt(N) queries:
Go through all the remove operations (query type '-') and, if possible, remove those numbers from the active set of numbers, and add them in a temp. set. This loop will take O(sqrt(N)).
Let currGcd be the gcd of all the keys in our active set. There are at most O(N) of them.
Process the chunk again and take 2 cases:
The answer for every query will be the gcd of all the keys in the temp. set and our currGcd. There are at most O(sqrt(N)) items in the temp. set, so this loop will take O(N).
At the end of a chunk, move all the items from the temp set to the active set (and clear the temp set).
The overall complexity is O(N * sqrt(N))
можно хранить наши элементы по блокам (gcd всех элементов в нем) + хранить мапу, где запоминаем, в каком блоке лежит число, для ответа пройдемся по блокам и пересчитаем gcd, для добавления/удаления пересчитаем gcd только в одном блоке код
It easily solves with segment tree, each leaf node stores x, non-leaf nodes gcd of its children.
Are Mo Algorithm and SQRT decomposition considered the same?
In SQRT decomposition we divide the array in buckets, solve the task in these buckets and answer each query in O(
buckets, solve the task in these buckets and answer each query in O( ) time (worst case). However, using Mo Algorithm the queries are sorted according to the bucket the left end of the queries falls into ...
) time (worst case). However, using Mo Algorithm the queries are sorted according to the bucket the left end of the queries falls into ...
I think both methods have the same time complexity, but are they considered the same?
SQRT decomposition combines several approaches and algorithms. Mo Algorithm is one of them.
SQRT Descomposition is a data structure, while Mo's Algorithm is more a technique.
Not really much of a proof. SQRT-decomposition on queries isn't so much of a data structure, but is still usually meant to be called SQRT-decomp
I got stuck with the problem 446C — DZY Loves Fibonacci Numbers and here's my submissions
could someone help ?
thanks in advance
Can 13E - Holes solved using MO's algorithm? Or There are other kind of Sqrt-Decomposition? I have solved the first two in the list. But can't find an idea about this one.
You know what, there is this thing called editorial for (almost) every round which explains how to solve the problems.
Thank you. I read the editorial before the comment. But their solution doesn't feel like the MO I learnt. And this problem is listed here. So I asked here if the solution is general, there might be some name or insights available that I want to know before solving it.
It is explained there 23:05
Thank you. I will take a look.
242E - XOR on Segment can also be solved with SQRT-decomposition. Although it's slower than the intended solution, it can still AC.
One more very nice SQRT-decomposition problem I encountered at the Innopolis Open Elimination round (2016-2017): http://codeforces.com/gym/101182/problem/E
Why i am getting TLE at 220B - Little Elephant and Array? My Submission 29417078 .Could anyone help me!
Edited: I have changed my solution from map to array.But this also gives me a TLE! 29417554
Maybe you have to create a struct for the query, add and remove method you can improve it because you have a lot process and you can put this in you cmp.
https://www.codechef.com/AUG17/problems/HILLJUMP Another good problem on this topic.
It's great to see guys like you guide beginners like us ! Thank you so much !
446C DZY Loves Fibonacci Numbers gives TLE with sqrt decomposition. My code gives TLE although its complexity is O(N*sqrt(N))?? Any help would be appreciated.
I don't find your mistake, but i know easier way to solve it.
See my code.
Main idea : divide queries in sqrt(m) blocks.
I saw your code. Your Idea is cool. But your code and mine have literally the same complexity.
Change long long to int I was also getting tle on this problem because of this
Another good problem on this topic: Chef and Graph Queries
It's solvable by MO or Sqrt-Decompositon or both? In any of the cases, can you tell me your approah?
Another one: Chef And Easy Xor Queries
I solved Timus 1390 using SQRT optimization
How to solve 506D using SQRT decomposition. I've solved it using DSU
I just ACed 446C using segment tree with ~2s time. I wonder how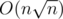 algorithms can avoid TLE
algorithms can avoid TLE
prolly coz sqrt decomp is more cache friendly?
another problem on this topic: here
Problem D
I have started learning this technique just now. Can somebody suggest some beginner friendly problems on this concept. Any platform would work, Codeforces, Codechef, GFG, SPOJ, any.
You can try solving first problem (Little elephant and array)
Alright, Thanks for the suggestion. Do you have any more problem suggestions
i just learned it, i have solved the first 2 problems till now.
sqrt solution of 444C — DZY Loves Colors.. not by me .. code