Hi! Modular inverses are used in the solutions to a lot of number theory problems, such as 622F - The Sum of the k-th Powers from the latest educational round. I want to share a one-liner (essentially) that computes modular inverse with the same complexity as the exteneded Euclidean algorithm (a and b are supposed to be positive co-prime integers, and inv(a,b) is the inverse of a modulo b, lying between 1 and b):
long long inv(long long a, long long b){
return 1<a ? b - inv(b%a,a)*b/a : 1;
}
The idea behind the code is that to compute inv(a,b), we find x such that  and
and 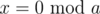 , and then return
, and then return x/a. To find x, we can write x = yb + 1 and solve for y by recursively computing inv(b,a). (Actually inv(b%a,a))
This isn't the fastest method if you're worried about performance, and you will probably get overflow if a*b doesn't fit inside a long long. But I think it's neat.











Another idea for calculating inv( when b is prime ):
This can work because inv(a,b) is a^(b-2) ( b is prime ).
Shouldn't the code be
http://e-maxx.ru/algo/reverse_element
Note that here we have taken inverse wrt b in both the case that is a and b%a and not wrt a in case of b%a as mentioned in the blog so shouldn't the code be the following when taken wrt a ??
What do you say?
That's clearer since there's no remainder in the division, and reading it modulo b you just get 1/a. But it's equivalent to what I wrote when a>1, if you do integer division.
Ok, So you are taking advantage of C++/Cpp rounding towards zero.And since -inv(b%a,a) is negative and [1-inv(b%a,a)*b]/a will be same as -inv(b%a,a)*b/a. When I first saw it, I was confused so I have written the above comment. I got it now. At least I have learned two ways of finding the inverse. Thanks. Learn and Let learn.
Another idea for calculating inv( when b is prime ):
int inv(int a,int b){ int ans=1; int mod=b; for(b-=2;b;b>>=1 , a*=a , a%=mod) if(b&1) ans*=a,ans%=mod; return ans; } This can work because inv(a,b) is a^(b-2) ( b is prime ).
Water is wet, Mr. Obvious.
So the final code snippet is
This code is conceptually clearer. But I don't understand why so many downvotes. Beautiful Codes are MUCH better than 'Shorter' ones!