I apologize for the mistake in the constraints of problem J, and for my bad English.
Problem A: Random Fightings:
DP[i] is the probability that mask i (i.e. the people whose indexes are equal to 1 in mask i) are still alive.
DP[2n - 1] = 1
For each mask, for every pair of alive gangsters (i, j), calculate the probability of gangster i dying in the next fight against gangster j, let us call it p, and add p * DP[mask] to DP[mask - 2i] (i.e. the same mask but with the ith bit switched to 0).
How to calculate p?
p is the product of the probability of the jth gangster killing the ith one if they fight each other (Aji) and the probability of having a match between them.
The number of possible matches for a mask is x * (x - 1) / 2 where x is the number of alive gangsters, therefore the probability of having a match between them is 2 / (x * (x - 1)).
Problem B: Rectangles:
You need to cover all x s and y s, therefore the rectangle should cover all points from (minx, miny) to (maxx, maxy).
The area is (maxx - minx) * (maxy - miny)
Complexity: O(n)
Problem C: Too many coins:
Sort the types of coins in decreasing order by the amount of each type (the product of the value of the type and the number of coins of this type), and if there is a tie the larger value comes first.
Then, start adding the types one by one until the sum is greater than or equal to M.
Complexity: O(ClogC)
Problem D: Card Game:
Binary search the answer, to check if it is possible to distribute the cards such that the maximum power is less than M, keep giving cards to the first player while his power is less than M, then move to the second player and so on. If at the end you were able to distribute all the cards, then it's possible.
Complexity: O(nlogn)
Problem E: Xortion:
a xor b$ is maximal when the ith bit in a is not equal to the ith bit in b.
Since 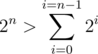 , we should try to match each bit with it's opposite greedily starting with the most significant bit.
, we should try to match each bit with it's opposite greedily starting with the most significant bit.
Build a trie that consists of the binary representation of each number, starting from the most significant bit.
For each query with number x, go through the trie matching the most significant bits first.
Problem F: Print mix strings:
Generate all possible strings:
void generate(int i,int j,string res)
{
if (i==a.length() && j==b.length()) // no more letters left, add the string to the set of possible strings.
s.insert(res);
else
{
if (i<a.length())
generate(i+1,j,res+a[i]); // add a letter from string 'a'
if (j<b.length())
generate(i,j+1,res+b[j]); // add a letter from string 'b'
}
}
Problem G: Count mix strings:
The resulting string will have length n + m, and you want to fill it with two types of letters, letters from the first string, and letters from the second string. You can consider letters from the same type identical, because there is only one way for the relative order of letters from the same type (they should remain in the same order as the original string).
So we need to choose n indexes from the n + m indexes available, and fill them with letters from the first string, and fill the rest with letters from the second string. Therefore the answer is:

You can precalculate all i! mod 109 + 7 for 1 ≤ i ≤ 20000 and use modular multiplicative inverse to find the answer:
(((fact[n + m] * inv(fact[n]))%MOD) * inv(fact[m]))%MOD where fact[x] = x! mod 109 + 7 and inv(x) is the modular multiplicative inverse of x.
Problem H: Tourists:
We need to find a solution for the equation: x * n1 + y * n2 = n such that x * c1 + y * c2 is minimum.
The equation can be solved only when n is divisible by gcd(n1, n2).
We can use the extended euclidean algorithm to find a solution to the equation a * n1 + b * n2 = gcd(n1, n2), if we multiply this equation by n / gcd(n1, n2), we get: (a * (n / gcd(n1, n2))) * n1 + (b * (n / gcd(n1, n2))) * n2 = n
Therefore: x = a * (n / gcd(n1, n2)) , y = b * (n / gcd(n1, n2)).
After finding this solution, the other solutions would be:
X = x - r * (n2 / gcd(n1, n2)) , Y = y + r * (n1 / gcd(n1, n2))
If the cost per passenger of the first boat is less than the cost per passenger for the second boat, we should try to maximize X, while keeping Y positive. to do that we can find the minimum r which makes Y positive by binary search.
Otherwise we look for the maximum r which makes X positive, also with binary search.
Problem I: Teleportia:
Build a directed graph of n + 1 nodes: The stations, the starting and the ending points. The distance between node A and node B is the manhattan distance between the 2 points, or min(2, manhattan distance) if A, B are stations, and B is a target of A. After that, Apply Dijkstra from the starting point to get the answer.
Complexity: O(n2log(n))
Problem J: Palprime:
between 1 and 221 are about 210 binary palindromes, generate all of them, store the ones that are prime numbers in a set, then answer each test case with binary search.










G. Let a be the length of the first string and b be the length of the second string. Then the number of ways is just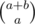 .
.
I solved problem G with one standard DP approache — like recoursion in problem F — Dp[i][j]=Dp[i-1][j]+Dp[i][j-1]. We have enough memory and time for it.
Also I didn't do contest all the time and with full speed, but I found some interesting and new tasks for me. Thanks!
I had a template on Exponentation by Squaring and nCr before the contest, but apparently I only realized this problem ~35-36 mins after contest starts. This problem can be solved in O(min(a, b)logp) where p = 109 + 7.
Actually, you don't have log factor. First calculate all factorials in interval [1,a+b], after that calculate needed powers for inverse values. Total complexity O(a+b).
Can memory limit be satisfied for building a trie in problem E?
UPD: I got that, Thanks.
Can you give me the code of H,or see my code:http://paste.ubuntu.com/24199065/
This is my solution: http://pastebin.com/ei4w5zRU
thanks, But I want to know how to solve it by bound search correct