Inspired by 163B - Lemmings.
Let us have an unknown rational number presented as an irreducible fraction 0 ≤ p / q ≤ 1, where denominator does not exceed Q (in this task — 109). We have a function which determines whether given rational number is less than, greater than or equal to that unknown number (intf (p, q) → {1, 0, - 1}). The problem is to quess an unknown number using only f(). It is impossible to call f(x, y) where either x or y exceeds Q. Floating point arithmetic is also prohibited. How fast can this problem be solved? Usual binary search is impossible, because it uses rational number's value but not it's numeric representation.
First idea: iterate through a denominator's value and find a numerator using binary search. Asymptothics is O(Q·logQ), which is too slow.
Second solution uses Farey series idea and binary search idea too. Assume we have an interval which contains an unknown number bounded by pl / ql и pr / qr, initially equal to 0 и 1 respectively. On each step find pm / qm, where pm = pr + pl, qm = qr + ql, calculate f(pm, qm) and continue doing this with left or right part of an interval respectively. In at most q steps we should get a required fraction (it's easily prooved using Farey series). Asymptothics is O(Q). I want to have O(logQ) or at least something sublinear (o(Q)).
I think, that this problem is rather old and stupid and I reinvent the wheel solving it. How can it be solved?











I happen to know this problem, it is very nice.
I do not really want to spoil it for you, so here is a hint: think of your traversal of the Farey sequence (or equivalently, the Stern-Brocot tree) as a sequence composed of letters L and R. As you noticed in the second solution, the length of this sequence can be Θ(Q), so we cannot just follow it naively.
However, what if the sequence consisted only of Ls (or only of Rs) — that is, if we never changed the direction of our traversal? There exists a faster solution then. Try to generalize it for all sequences.
I've already posted this link in a Russian comment. It describes a solution which works in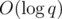 time.
time.