→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 17:51:18 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Problem 450 is very creative:
Ok, more serious now: if we don't use the above theorem, what is expected solution? I can only think of brute force 1 spanning tree & check if another exist, but the complexity in worst case is N(N - 2) * N2 = NN which seems too big..
I randomly generate a permutation of m edges and greedily (like Kruskal) find a spanning tree, then check if the remaining edges are valid. I do this for 300000 times and it passed ST. Maybe it's hard to generate testcases against this approach.
If there is a solution with 18 edges, then any random permutation where the 9 edges belonging to the first partition are before the 9 edges of the second partition works. The probability of getting permutation like this is at least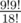 . Therefore the probability of failing if you do 300000 iterations is at most
. Therefore the probability of failing if you do 300000 iterations is at most 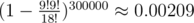 .
.
Since you only need two trees you can do this
iterate through the edges and hold 2 dsu's
assume that the edge is u-v if find(u, firstdsu) == find(v, firstdsu) then we do not need this edge in the firstdsu and we will use it in the second dsu
likewise if find(u, seconddsu) == find(v, seconddsu) we just merge(u, v) in the first dsu
if neither of these happen we just check the both ways (adding the edge in the first dsu or the second one) since this doesnt happen more than 2 ^ (2n — 2) (the number of times we get an edge that reduces the number of components) times we can say the program is of O(2 ^ (2n — 2) * m * dsuOperation)
I just have to comment by saying this is an awesome solution. It almost makes me not angry by the fact that this was a googleable problem :P
thanks that makes me pretty happy :D
Didn't understand :| A little explanation please?
i edited my explanation maybe it was because of the typo's (either -> neither) if you wanted more explanations please tell
I believe the intended solution is bell-number DP.
For example, dp[{{1, 3, 6}, {2, 5}, {0}}] is true iff we can divide edges among {0, 1, 2, 3, 5, 6} into two groups such that
This solution will work in O(bell_number(N) * poly(N)).
Hmm, I'm a bit surprised that no one mentioned the intended solution. Note that both testers come up with that first. (EDIT: it was mentioned above by Reyna)
Consider edges one by one, each time you have 2 choices: add it to graph 1 or graph 2.
Note that if add it to graph 1 no longer reduce the number of connected components, but add it to graph 2 can reduce the number of connected components, then we just add it to graph 2.
With this pruning, the running time will be O(C(2n, n) * m).
This was mentioned above by Reyna and it think it's pretty cool.
However, I'm wondering whether anyone tried to google this problem during testing?
I Googled it with keywords like "split graph into two connected graphs" and so on, instead of searching things related to "spanning tree".
If I understand correctly, the problem was to find 2 non-intersecting trees in a graph. It can be solved in polynomial time. Moreover, finding k non-intersecting trees can be done in time of (nk)^3.
We can think in a problem in such way. Lets color each edge in it's own color, and copy graph k times. Then we need to find acyclic subgraph in which all colors are different. Both this conditions on sets form a matroid.
We can find biggest set which lies in two matroids using matroid intersection algorithm
Nash-Williams-Tutte's theorem, afaik. Here is some paper.
Yeah, for me the algorithm of solving this problem was
Looks like problem setter was studying spanning tree theorems when he came up with this round...
For div1 450, I thought about partitioning, but I only considered partitions into 2 sets and checking if edges between partitions were at least 2, not all partitions... I doubt I would be convinced that it would work even if I thought of the all partitions idea.
Is there a way to check who is the author of this contest? It contained some graph problems that I found very interesting, so I want to check his previous rounds on CF/TC.
cgy4ever
https://community.topcoder.com/tc?module=ProblemArchive
You can get this page by click 'Problem Archive' in Dashboard (the default page after you login).
The hard problem is exactly the same as this one(in Chinese).
Thanks for the info. That explains why matthew99 can solve it so quickly. :)
And it seems I need to read all tasks in that OJ.
cgy4ever What is the problem in running simple dfs for div 2 500 ? My solution with simple dfs. I find many submissions getting wrong answer for this. Can you please explain what is the right approach for this problem ?
"Simple dfs" is essentially a greedy solution. You visit each vertex at most once and if you were not lucky enough to find the correct path at the first try you won't ever consider other paths to a vertex. A small counterexample is
As is often the case, dynamic programming works in this problem while greedy does not. Try to find a state of the form (last_visited_vertex, something_else).
UPD. I've read your solution one more time. What you wrote is in fact a backtracking solution that has a misleading name 'dfs'. Your mistake is probably that in some cases you forget to set back vis[u] to false in the loop. Such exhaustive search should not work for this problem because of its high time complexity but the top-scoring solution suggests that it could work if you add some pruning.
Could you solve this problem by using Dijkstra's algorithm on the first graph, then follow the same path for the second graph?
Shortest path in one graph will not lead to optimal answer (least product of total path length in two graphs). Hence this strategy won't work. As the constraints were small, I used floyd-warshall algorithm to solve it.
Where does one public editorials on topcoder.com ?
http://apps.topcoder.com/wiki/display/tc/SRM+685
Can anybody please explain, how to solve div 2 900?
Dynamic Programming or Memoization with BitMasks.( E * (2 ^ N) * (5 ^ 3) )
State is (msk,r,g,b). Your return value is a boolean.
The mask represents nodes with degree bigger than zero.
Suppose we have an edge connecting nodes u and v.
An edge can only be added if at least one of deg(u) or deg(v) is zero to maintain growing a spanning tree. (
We can only have up to (n-1) / 3 edges of each colour given the constraints, both r ,g and b cannot exceed 5. ( otherwise we just prune this impossible state. 2^13 * 13 * 13 * 13 will give MLE ( Java ) ).
In our DP:
Iterate over all edges, if it’s possible to add this edge, set both nodes it connects to 1 in the bitmask, increase r,g or b depending on the edge’s colour.
After each step recurse further.
Base case: When mask contains n 1’s it means we have used (n-1) edges which means our tree ready. Check if every colour in our state equals k / 3.
Another solution for the problem could be something like this :
Let us fix a root for the final spanning tree and to every other vertex assign a color (among the R/G/B). Since the root is fixed, we can associate each vertex with an edge (connecting the vertex with its parent) and assigning color to the vertex can be thought of as assigning color to the corresponding edge. Given such a configuration (a fixed root and a color for each node) we can check using simple bfs whether such a spanning tree is possible or not by starting at the fixed root and exploring only those edges which have the same color as the vertex explored by those edges.
We can check all possible configurations which turns out to be O(n*3^(n-1)*|E|) which looks pretty large but since we need to check only those cases where number of edges of each color is same, a lot of the search space is pruned and it works well in time. You can have a look at this accepted solution for more details :
http://pastebin.com/nhiNXWFq
Does anybody have the solution for div1 hard which he can prove?
Can anybody tell the idea of the problem?
Does it has something to do with eigen values of the Laplacian matrix?
I haven't implemented it but I guess we can do the following:
Let g be the primitive root of 109 + 7.
For each x = g0, g1, ..., g29999 and x = g0, g30000, ..., g999990000 generate a tree with up to 150 vertices and x MSTs. (I'm not completely sure but we can find these trees like the original problem)
Connect them with an edge.
Yes, that would lead to a proof that is 'not too long'. (obviously you can run your program for all 109 + 7 inputs to get a proof, but it may take years.)
My proof is like this:
Generate 20000 random graph with 10 nodes, for each of them compute Discrete logarithm of number of MST, so we get a list of 20000 numbers.
Then for each pair of number in this list, add sum to a new list, so we get a new list of 200002 numbers.
Find the minimal gaps between numbers in that list. In my case, it is 118.
So my graph will have no more than 10 + 10 + (118/3) * 5 + (118%3) * 5 = 220 nodes. (A cycle with length 5 has g1 MST, and a clique of size 5 has g3 MST)
My program needs to run about 2 minutes with 2GB of memory.