Hi.
As always the question can be stated fairly easily:
Given a set of points on a 2D plane, how to find a point (x, y) on that plane such that sum of the euclidean distances between the chosen point and the given points is minimum (among all possible choices of (x, y))?
How about finding the same thing in a 3-Dimensional space?
Thank you for the time you put on reading this and thanks in advance for sharing your solution/idea.











I misunderstood the problem, Ignore
wtf?
I meant you don't care about the points in the set which are inside the convex hull.
It's so because the diameter will always be a pair of the Convex Hull's vertexes.
But the diameter has nothing to do with the problem in this entry...
Lol, just understood that I misunderstood the problem :D
Sorry the solution is to a completely different problem.
You minimize the maximal distance between the center but not the sum of them. The solution of the original problem is to run two ternary searches: on x and y coordinates, one into another. The proof is based on the fact that the sum of the convex functions is a convex function.
Should the two ternary searches be independent or should they be nested?
When in the first ternary search you fix some x, then you run ternary search on y in fact on the segment [(x, - ∞), (x, + ∞)].
Thanks. That does the job.
Why is simple ternary search the bad idea?
This would mean that the point we are looking for is (x, y), where x and y are the "center"s of the projection of the set of points onto the x axis and y axis respectively. Right? Can you prove the correctness?
Distance to some point is convex function. Sum of convex functions is also a convex function. Isn't it enough?..
Yepp it is. Thanks.
This point is called Fermat-Weber point. For n=3 we get famous Torricelli point. But in my opinion for other n it is #P complete problem.
But anyway, for each ε there exists an algorithm polynomial on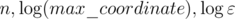 , finding the point with precision ε. I think that for ε = 0 you simply can't output precise answer, when it is irrational, so I don't think we can consider this problem as a #P problem, or we need to find a way to express the answer in the other form.
, finding the point with precision ε. I think that for ε = 0 you simply can't output precise answer, when it is irrational, so I don't think we can consider this problem as a #P problem, or we need to find a way to express the answer in the other form.
What if we want to find one of the given points that have minimum sum?