Hi everybody! FYI, 1st Qualification Round of RCC starts in less than an hour. I still don't see any kind of announcement on CF, so let it be here.
Good luck!
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 2 | adamant | 164 |
| 4 | TheScrasse | 159 |
| 4 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Hi everybody! FYI, 1st Qualification Round of RCC starts in less than an hour. I still don't see any kind of announcement on CF, so let it be here.
Good luck!
| Name |
|---|



http://www.russiancodecup.ru/en/
How to solve D faster than , where n = 5 * 105?
, where n = 5 * 105?
I didn't submit it during the contest, not sure if it would fit the TL, but an O(n*sqrt(n)) solution would be to maintain an array of answers for all k; initially it can be built in O(n*sqrt(n)), then updated in O(#divisors(T[v])) for each query of type 1 and 2.
It may be solved in O(n * sqrt(MAX) + m * numberofdivisors(MAX)) where n = m = 1e5
Maintain all answers, changes are O(divisors), queries are O(1), precalc is O(n * sqrt(MAX)): for each problem you have O(sqrt(MAX)) ranges to add fixed value. It may be done offline without log
PS: had to spend much time to fit in TL anyway:(
It seems we need a faster solution: http://codeforces.com/blog/entry/44604?#comment-292931
How to solve B?
First and last carriage should be lit
Its not THAT simple :D
we should make the procces using deque. If we can we push the carriage to the tunnel. If we can't we delete first carriage from tunnel. And we should keep the amount of lights. If current lights is zero. We make the last carriage lighting. And in the end we should delete all the carriage from the deque.
Here is my code
Sorry for my english
An easier solution, just use a variable sum My code
I did the same, but got WA :(
Greedily + check first and last carriage for light http://pastie.org/10829451
Has anyone solved C faster than O(n * maxdivisor * logn)?
Well, I don't know an actual complexity of my solution, but I couldn't come up with a test to make it work at least observably long.
(Copy-Paste from another thread on CF):
Magical solution for C. Divide all numbers by their common GCD. Now it's easy to see that the answer is no less than 1 and we should check if it's at least 2, and if yes, find it. Let's calculate the following "DP": iterate over numbers, when passing the i-th number keep set of pairs (a, b) where a and b is the pair of gcd values we can achieve by splitting first i numbers into two sets. When passing the number x, we take each pair (a, b) and form two new pairs (gcd(a, x), b) and (a, gcd(b, x)).
It is now working in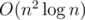 , but we make a super-observation that we are not interested in pairs where one of the numbers is equal to 1 since we already know that the answer is not less than 1, they provide no information for us. Do not add such pairs and it gets AC. I have no single idea WTH it works. Maybe because I sorted all numbers in increasing order and uniqued them?
, but we make a super-observation that we are not interested in pairs where one of the numbers is equal to 1 since we already know that the answer is not less than 1, they provide no information for us. Do not add such pairs and it gets AC. I have no single idea WTH it works. Maybe because I sorted all numbers in increasing order and uniqued them?
I also don't know the complexity of my solution. I came to idea that first element in any case will be in one of two group. So we can go through all of his divisor and iterate though other elements if element also has this divisor we put him in one group with first, else we put him in another group and keep the gcd. This solution got TL
I decrease the time, using one if. if current gcd of second group is smaller than our current maximum we break;
Here is my code
Is it possible to upsolve the problems?
Solution for this round Tutorial
Can someone pls make a training for it here? :)
We have something for you: 2016 Russian Code Cup (RCC 16), 1-й квалификационный раунд :-)