Hi, everybody! Recently, I tried to solve a problem. In this problem I had to determine, is number N sum of two squares? i.e. N = a2 + b2?, where a and b are integer. N < 1015. Firstly, I tried to brute-force a and check N - a2 for a square, but got TL. Also I tried to factorize the number and check degree of prime divisors p = 4k + 3 and used Fermat-Euler theorem to check the fact. But also I got TL. I suppose this problem to solve with number of operations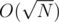 
. And I'm interested in technical realization of it. Can anybody show how to write accurate brute-force or factorization for example on C/C++? And what advices can you give to write same programs, making as less operations as possible? It's the problem from acm.timus.ru link here Thanks in advance!
→ Pay attention
Before contest
Codeforces Round 940 (Div. 2) and CodeCraft-23
3 days
Register now »
Codeforces Round 940 (Div. 2) and CodeCraft-23
3 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/19/2024 04:30:03 (i2).
Desktop version, switch to mobile version.
Supported by
How can you use an algorithm that checks
N = a²+b²in the problem you linked? It asks for the minimum number of squares that sum to N, am I right?a little hint
http://en.wikipedia.org/wiki/Lagrange%27s_four-square_theorem
Any natural number can be represented as the sum of four integer squares. We check that N = a2. If not, we check that N = a2 + b2. If this is not correct, we check that N = a2 + b2 + c2. And the answer is 4, if this is also not correct.
how can we check if N can be represented as a sum of three squares fast?
The following question on MathOverflow might help: http://mathoverflow.net/questions/57981/testing-whether-an-integer-is-the-sum-of-two-squares
EDIT: Sorry, I misread your comment :)
IMHO, in that problem more easy to check if N can be represented as sum of 1,2,4 squares. Else — 3. :-)
27 = 1*1 + 1*1 + 3*3 + 4*4 = 1*1 + 1*1 + 5*527 != a*a27 != a*a + b*bFail.
if N != (8*t+7)*4^k then there are 3 squares.
oh, don't you know the proof or some link with the proof?
And now read your previos explanation.
sorry, I've misunderstood you
It returns 0, if x is not a sum of three squares.
How come?
This is a very difficult method of pen and paper :)
I think that algorithm follows this: http://www.proofwiki.org/wiki/Integer_as_Sum_of_Three_Squares
For sum of two squares, how can it be modified?
Don't answer him. This is one of the problems from a running contest.
Sorry?
Motori
according to me we can run a loop in which 'i' goes from 1 to sqrt(N/2) and if N-i*i is a perfect square we are done....
for(int i=1; i*i<=N/2; i++) { if((N-i*i) is a perfect square) done; }
its complexity is O(sqrt(N)).....
How do you check number for square? I did the same and used sqrt() and got TL.
An arbitrary positive number n is expressible as the sum of two squares iff, given its prime factorization
n=p1^(a1)p2^(a2)p3^(a3)...pk^(ak),
none of pi^(ai) +1 is divisible by 4 (Conway and Guy 1996, p. 147). http://mathworld.wolfram.com/SquareNumber.html