Today, 20:10 MSK
→ Pay attention
Before contest
Codeforces Round 940 (Div. 2) and CodeCraft-23
43:04:23
Register now »
Codeforces Round 940 (Div. 2) and CodeCraft-23
43:04:23
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 2 | adamant | 164 |
| 4 | TheScrasse | 159 |
| 4 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/19/2024 22:30:38 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











How to solve 500?
Динамика. Прошли i рек, оказались на такой высоте. Переходы либо на 1 вверх по суше, либо по морю. Это какой-то len^2*m. Осталось заметить, что работают два указателя, потому-что что-то выпукло куда-то.
Вечный вопрос: а как заметить что "что-то выпукло куда-то"?
Ну это же корень. Он всегда выпуклый. Дальше надо пописать какие-то оценки и увидеть, что если нам сейчас выгодно опуститься на 1, то в прошлый раз это было еще выгоднее. А еще почему эти коментарии на английском? Пошли в другую ветку.
Мое решение на чем сломал? TL?
Да. Просто вбил большой случайный тест. С учетом того что тернарник казалось бы вообще не работает, на чем-то бы свалилось.
// эта ветка — английская.
Сразу скажу, что сам не успел дописать задачу.
Я заметил это так: нарисовал карту, хочу пройти в точку (x, y) из (x - 1, 0). Тогда я могу в неё попасть тремя способами: пройти по острову x - 1 расстояние y, затем по воде (получается перпендикулярно) расстояние width[x - 1], пройти по воде перпендикулярно расстояние width[x - 1], потом по острову x расстояние y, причём эти два значения будут равны (думаю, что это очевидно), либо пройти по "гипотенузе" расстояние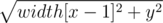 . А потом вспоминаем, что в прямоугольном треугольнике длина гипотенузы всегда меньше суммы длин катетов, ну и интуитивно понимаем аналогию.
. А потом вспоминаем, что в прямоугольном треугольнике длина гипотенузы всегда меньше суммы длин катетов, ну и интуитивно понимаем аналогию.
P.S. Понимаю, что сказал полный бред, но это были всего лишь мои мысли :)
Alternative solution. At first assume we got from 0, 0 to sumWidths, 0. Take this time as an answer. Then length times do following — increase difference between indices of source and destiantion ports on some river (or walk 1 segment anywhere). Choose river where such operation would lead to smallest increase of answer. Notice that for this river next increase would be bigger, so our algorithm is correct
А еще оказывается работает решение добавить подъем на 1 там где он меньше всего нагадит length раз. Видимо опять таки из за того что корень — очень хорошая функция.
Если быть точным, то потому, что в каждой реке это число увеличивается после операции
А почему из того, что для каждой речки это число увеличивается, следует, что такая стратегия оптимальна?
Потому, что мы тогда возьмем length самых маленьких чисел
Спасибо, понятно
Another alternate solution. This problem is equivalent to knapsack problem (we want to take L meters up). So we have width.size() + 1 of objects, width.size() of there is rivers and one is the object that correspond to moving up (his width is 0, and his speed is walk). So we can proof that it's possible to solve this problem in such way: For all objects put into array L values timeToGo(width, Y+1, speed) — timeToGo(width, Y, speed) (1 <= Y < L), than sort this values, and sum first L values from array.
So this sum is the answer to the problem without sum for all rivers timeToGo(width, 0, speed).
timeToGo(w, y, s) = sqrt(w*w + y*y) / s.
My solution (Java) with 1 * n * length sqrt calculations works appr. 2 seconds and was challenged (got TL). I suppose it would get AC written in c++. The question is, how to avoid such number of sqrt's? Am i missing something?
UPD. It got TL as I forgot to cast width[i] * width[i] so there was an overflow, and NaN values produced time limit on max test. With cast it works about 300ms, which is totally comrehensible.
Egor's solution requires only O(n + length) square root calculations for example.
Yes, and that solution is great. Mine dealt with two pointers, and I already found a couple of java solutions with almost the same code which passed systest, so anyway it's my fault.