Block Tree
Story
I was trying to solve this problem from the gym and I struggled to find the solution. Finally, I came up with a very interesting data structure capable of handling any subtree update and really don't know if someone else has seen it before, but I will post it here since I could not find its name (if it has) in google. My solution was able to solve the problem with O(N) memory, O(N) in creation,  per query. When I saw the editorial I saw that it had another interesting approach with an update buffer which solved the problem in
per query. When I saw the editorial I saw that it had another interesting approach with an update buffer which solved the problem in 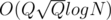 , for my surprise my solution was
, for my surprise my solution was 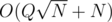 summing the creation and queries, and I saw conveniently the author used Q < = 104 so probably the author didn't know about my approach.
summing the creation and queries, and I saw conveniently the author used Q < = 104 so probably the author didn't know about my approach.
After analyzing my approach and reading one of the comments in the same problem, I saw that the problem could be also solvable using Square Root Decomposition in the Euler Tour Technique. Then I analyzed my approach and it seems that they are 90% the same, but the difference is in how the decomposition is stored. As some can see the relationship between KMP and AhoCorasick (Matching in Array — Matching in Tree), I see this as (Sqrt Decomposition Array — Sqrt Decomposition in a Tree). So, after posting this structure I search in what cases is my data structure better than the Euler Trick, then I thought of a new feature that can be implemented. I found it, it can dynamically change (be cut, and joined). Well, I probably have bored with this story, so let's go to the point.
Update — After posting this algorithm I received a comment with the name of this structure, it is called block-tree for those who don't know. I tried to find something on the internet but with no success.
Construction
The idea is not very hard, first do a dfs to compute subtree size and depth of each node. Order all nodes by depth in reverse order, this can be done in O(N) using counting sort. We will now create what I called fragment, we will collect small tree-like portions of the tree and assign them to fragments. The subtree size will be modified in each iteration it will count how many subtree nodes are not inside assigned to a fragment. So, each time we start with a node we shall update its subtree size, after that iterate its children again and count how many children are not assigned to a fragment, after this count reaches  , we create a special node and assign the children to this new node and remove the children from the previous parent.
, we create a special node and assign the children to this new node and remove the children from the previous parent.
for(int u : orderedNodes){
SZ[u] = 1;
for(int v : adj[u]){
SZ[u] += SZ[v];
}
newAdj = []
temp = []
spNodes = []
int sum = 0;
for(int v : adj[u]){
if( sum > sqrt(N) ){
int sp = createSpecialNode(u, temp);
spNodes.push_back(sp);
temp = [];
SZ[u] -= sum;
sum = 0;
}
}
adj[u] = concat(temp, spNodes);
}
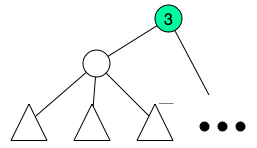
After this I will end up with  groups.
groups.
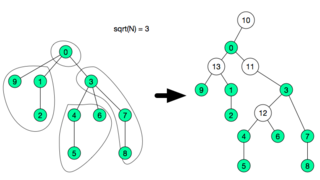
here each special node needs to be able to answer any query or update in O(1). Since the fragment is very small 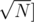 if O(1) is not possible, any other structure used in that subtree will be relatively efficient since it will be
if O(1) is not possible, any other structure used in that subtree will be relatively efficient since it will be 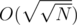 or
or 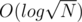 , although the time constraint will be very tight.
, although the time constraint will be very tight.
So, after this decomposition, we create a new adjacency list adjacencyList with these new nodes in O(N), and there will be  extra nodes. After that another adjacency list subAdjacencyList will be created in
extra nodes. After that another adjacency list subAdjacencyList will be created in  with the tree only consisting of the special nodes.
with the tree only consisting of the special nodes.
Proof of correct segmentation
I don't have a formal proof for correct segmentation, but in the construction above the ONLY way that I create a segment is only if by adding the subtree to the list it goes over  , and since the two groups of subtrees I am adding are less than
, and since the two groups of subtrees I am adding are less than  (if not they would have merged before) then each time I create a fragment it will be of size
(if not they would have merged before) then each time I create a fragment it will be of size 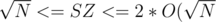 since ALL fragments have size
since ALL fragments have size 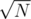 then the total number of fragments will be
then the total number of fragments will be
Unable to parse markup [type=CF_TEX]
. So segmentation is proven. If I am wrong in this informal proof, I am open to comments.Query
After the construction each query of subtree can be easily answered will be answered with a specialized dfs. The dfs will start on u and do one of two. If the node is special, then query the fragment in O(1) and recursively add the answers returned by dfs(specialChild) using the subAdjacencyList. If the node is non-special node, then apply any pending update in the fragment this node belong and query each individual node recursively using adjacencyList. It is not hard to prove that the fragment u belongs will be updated completely in  [as lazy propagation] then it will visit at most
[as lazy propagation] then it will visit at most  nodes in that same fragment and then it will query at most all the fragments. This leads to 3 time
nodes in that same fragment and then it will query at most all the fragments. This leads to 3 time  leaving a complexity of
leaving a complexity of  . This code is something like this:
. This code is something like this:
// G : fragment u belongs
// leader() : returns the leader of the fragment
Long getSum(int u){
if(leader(u) == u){
int fragId = fragmentOf[u];
Long w = frags[ fragId ].queryFragment();
for(int g : subAdjacencyList[ fragId ]){
w += getSum( frags[g].leader );
}
return w;
}else{
frags[ G[u] ].updateAllNodesIfPendingChanges();
Long w = u >= N ? 0 :V[ L[u] ] ;
for(int v : adjacencyList[u]){
w += getSum(v);
}
return w;
}
}
Update
If the update is in one subtree it can be done similar as the Query function with lazy updates in the fragments and active updates in  nodes. If the update is in all the nodes that are at distance L from the root (as in this problem), it is slightly different. For that we only need to iterate each fragment and update a value per level we have in that fragment (at most of size
nodes. If the update is in all the nodes that are at distance L from the root (as in this problem), it is slightly different. For that we only need to iterate each fragment and update a value per level we have in that fragment (at most of size  ) like this valueInLevel[L - leader.level] and update the value representing the whole fragment, in this case fragmentSum + = nodesInLevel[L - leader.level]. this will be done in O(1) time, for each fragment. This later update will be seen like this.
) like this valueInLevel[L - leader.level] and update the value representing the whole fragment, in this case fragmentSum + = nodesInLevel[L - leader.level]. this will be done in O(1) time, for each fragment. This later update will be seen like this.
void update(int LVL, Long v){
V[LVL] += v;
for(Fragment &f : frags){
f.update(LVL, v);
}
}
Cut/Join
Everything above is  per query, cut/join in a node is not that hard to do. For cut we will only split one fragment and add a new parentless special node. And for join we will assign a parent to that special node. This sounds as O(1), but since we need to update the old(in cut) or new(in join) parent of the cut node this will probably cost
per query, cut/join in a node is not that hard to do. For cut we will only split one fragment and add a new parentless special node. And for join we will assign a parent to that special node. This sounds as O(1), but since we need to update the old(in cut) or new(in join) parent of the cut node this will probably cost  . This sounds amazing, but there is one problem, each cut creates one special node. and the complexity of this whole structure is O(specialNodeCount) for query and update. So probably we will lose the efficiency with many cuts. To solve this, we take advantage of the O(N) creation time. Each time the whole tree has been cut
. This sounds amazing, but there is one problem, each cut creates one special node. and the complexity of this whole structure is O(specialNodeCount) for query and update. So probably we will lose the efficiency with many cuts. To solve this, we take advantage of the O(N) creation time. Each time the whole tree has been cut  times, we will rebuild the tree in O(N), so that it will recover again the optimal amount of special nodes.
times, we will rebuild the tree in O(N), so that it will recover again the optimal amount of special nodes.
Notes:
- The whole code can be seen in my submission here or here to the problem. Any tip or something wrong in this post, just leave a comment..
- Was said in comments that mugurelionut paper was the same, i thought that but then i read it carefully and they solve different problems.
- It seems there are people that knows this, waiting for some sources.











Auto comment: topic has been updated by cjtoribio (previous revision, new revision, compare).
Good stuff! I've seen similar ideas mentioned in mugurelionut's paper. Maybe someone can pinpoint to some other tasks using this idea?
Just saw the paper, the idea is very very similar, I would say the same. Alghouth I haven't read it, how did you found this paper?
I've seen it being referred in the 2015 Chinese Training camp paper, page 127 and recognized his name from the Romanian competitive programming folklore, so i went ahead and read it. On that paper there are some other tasks mentioned i think.
Just read the construction of the tree in the paper. It seems that both trees are different, however mugurelionut here seems to solve path provlems, but it cannot handle subtree problems, since there can be super-node sub-trees of the size O(N), But his idea is brilliant, his idea is very similar but oriented for problems on paths while the trees i proposed here are oriented on subtrees. Thanks for pointing his paper, now I know a new one :p
It's true that I mostly had path problems in mind when I came up with that idea, but it could also be used for solving some subtree problems, by taking advantage that every node has O(sqrt(N)) ancestors inside its "fragment" (to use your term). For instance, if you need to query/update the subtree of a node u, you could query/update the "special" node below u (if any), plus all the ancestors of u on the path from u to its "special" parent. This works because if there's any update at a node v below u (and in the same fragment), then u will also be explicitly updated, as being one of v's O(sqrt(N)) ancestors inside the fragment.
This is indeed true and very good approach. However this is (point update)(query subtree), as a sqrt-fenwick approach in a tree. But imagin I want to add X to all nodes that are at distance L below node u, this is what I call subtree updates. My structre can handle this without loss, but it is weak in paths. In example if you want to update a path and query subtrees it could work without loss but if the query is not in subtree but in paths, my structure will not just fit.
How did you come across the Chinese training camp paper? And, more importantly, were you able to translate it somehow? :) I can't seem to download it and I don't think there's any translation option while reading it online.
I think I solved one of the HackerEarth April Circuits tasks with exactly the same structure. https://www.hackerearth.com/april-circuits/algorithm/utkarsh-and-special-dfs/
Which one of the two, mugurelionut ? Or this one ?
Well, honestly I am a bit confused now. Maybe I'm missing something important, in that case sorry. I considered these two as the same idea based algorithms with some implementation differences, and I just recall the problem which can be solved with this idea. I certainly didn't use additional vertices though.
This is a case where they differ, if you have a tree of depth less than sqrt(N). They will only be a single super-node. The tree proposed by mugurelionut can still be used since the tree is sqrt(N) balanced, and a lot of efficient queries can be done in it, However some operations such as lazy propagation that needs to iterate through all the nodes may not work. Also, the cut/join functionality will not be possible since you will need to cut a tree that has O(N) nodes.
I composed problem B from last year's ACM ICPC SEERC contest (http://codeforces.com/gym/100818/attachments/download/3890/20152016-acmicpc-southeastern-european-regional-programming-contest-seerc-2015-en.pdf) with the data structure from my paper as the intended solution. The problem has many more updates than queries, requiring fast updates (O(1)), while the queries can be slower (O(sqrt(N)). I'm not sure if the data structure described in this post can be used efficiently for that problem, though, since the queries were path queries.
No, it is a little inneficient with paths, it is more efficient with subtrees. although if each small subtree is a special datastructure that can do paths in logN then you can achieve sqrt(N)log(sqrt(N)) for a path. Probably need link cut tree if want to mantain the breakability of the tree, or HLD otherwise. Haven't read the problem still, so dont know if it works. If neither works we can use your structure and be O(N0.75) per query, very bad indeed.
Today I was going to buy a bus-ticket for my mom and in my way I started thinking "We use segment tree or BIT (1D, 2D etc) to get the SUM of a subarray and we can update it. But what can we do if we need to do this for a subtree?".
I was thinking to ask some good programmers whether there is any problem or efficient technique to do so.
This may sound silly but trust me I am very happy as I am not an expert programmer and this matter hit my brain about 1-2 hours ago. Luckily I got my answer :)
Thanks for such a good post and forgive me for this stupid comment.
I find the idea as a whole very nice, but I think there exist constructions which make it fail. What your algorithm is basically doing is partitioning the tree into O(sqrt(N)) vertex-disjoint smaller trees, each with size O(sqrt(N)). However, there exist trees that can't be partitioned like that, like the star graph with N vertices. The best such an algorithm would achieve is one partition with sqrt(N) vertices and N — sqrt(N) other partitions, each with one vertex. Essentially, the method seems to fail when a node has too many children. Of course, for most arbitrary and even not-so-arbitrary trees it's fine, so implemented in a regular contest it should score many points. But there doesn't seem to a way to fix this O(N) worst case behavior. Perhaps the paper which bciobanu linked has a better answer.
I appreciate your interest, but you are wrong this is the number of fragments in a star graph: 1 node with 99,999 childs had 316 fragments exatly, ran with my algorithm. Take a time analyze a good case and try to break it. The thing is the tree can't be split as i describe without creation of special nodes. The paper linked by bciobanu assign existent nodes as super-nodes, but my graph will do somthing like thid in a star graph.
You are correct, I understood the algorithm in a wrong way. I will think it through more thoroughly.
I think, the title of the post ought to be "Unknown Data Structure" instead of "Uknown Data Structure". :)
Thanks i fixed it, you were right.
I was never implying his paper was solving the same problem as yours :<.
In any case, for the purpose of not wasting this post over some misunderstanding, i will describe an easy solution for the given task, achieving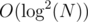 complexity per query.
complexity per query.
Start off with an euler tour of the tree. Let depth[i] be the depth of the node i. The arrays first and last will map a node back to its linerization positions.
We will use a 2D Segmented Tree to map points. We will map 2 * N points of type (depth[euler[i]], i).
Our update becomes: increase by Y the value of all the points with abscissa L. One can handle this with lazy propagation or using Fenwick trees.
Our query becomes a sum query in the retangle denoted by the top left corner (1, last[X]) and lower right corner (n, first[X]).
No, you did't imply this, :p I appreciated a lot your contribution the one that implied that was me. I thought it was the same, I just wanted to tell you that I was wrong, which is even better since now I have two cool structures. Sorry for the misunderstanding. Also cool solution in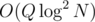 , euler toor seems very good. I am devising a little bit my idea but by sacrificing the ability of cut/join, I can generalize the proposed structure to
, euler toor seems very good. I am devising a little bit my idea but by sacrificing the ability of cut/join, I can generalize the proposed structure to  . Still need to work on it. But I like more the
. Still need to work on it. But I like more the 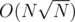 since it can be online. Once again i appreciated your referencing. I read it and it was very interesting Idea and could be even simpler to code than mine.
since it can be online. Once again i appreciated your referencing. I read it and it was very interesting Idea and could be even simpler to code than mine.
I think the idea in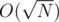 will be much faster (and also much easier to implement), because:
will be much faster (and also much easier to implement), because:
How will you make the 2D fenwick (you will need a map/unordered_map/hash table to store the values)? In such a way the complexity becomes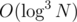 or
or 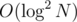 with a big constant. Also to make such "lazy propagation" you have a constant of 2d + 1 which isn't much if looked alone but when you combine it with the constant from the hashtable the solution becomes quite slow.
with a big constant. Also to make such "lazy propagation" you have a constant of 2d + 1 which isn't much if looked alone but when you combine it with the constant from the hashtable the solution becomes quite slow.
I think you misunderstood me. You will keep a segmented trees and in each node you will keep a Fenwick Tree capable of doing range updates and queries, not a 2D Fenwick Tree or whatever..
I think he said 2D segment tree incorrectly but he had a point. Each fenwick in each node if implemented naively it could lead to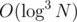 (map) or
(map) or 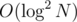 (hash, big constant). The fact is he didn't noticed that fenwick needs only to be of size
(hash, big constant). The fact is he didn't noticed that fenwick needs only to be of size
lengthOfSegmentCoveredand with arrays this is possible.Ok I got the idea but still I don't see a fast way to do this (the easiest I can think of is to save a treap in each node of the segment tree). If you use a Fenwick in each node you will encounter the same problem as the one I described in my previous comment (about the unordered_map/map/hash_table) and so the complexity again becomes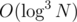 or with a big constant. The problem with the treap solution again is the same — a big constant.
or with a big constant. The problem with the treap solution again is the same — a big constant.
You will keep a sorted list of the ordinate keys in your node, like the merge sort tree. You will binary search the position of your query key in this list and then using the normalized index you will query the fenwick tree. This way you will avoid any shenanigans involving maps or hash tables.
Yeah I realized 2-3 minutes after writing the comment. Thanks :)
No need for binary search, the node of the segment tree can have the minimum and maximum depth of the nodes in this segment. so you will do if(maxL < L || minL > L) then you ignore this node even though it was in this query, and to query or update the normalize index will be L — maxL. The fenwick tree in that segment tree node will be of size maxL-minL+1
There is a solution I noticed, for this, if the segment tree has O(N) segments, adding their sizes is only in total. The fact is that each segment don't need a array from 0 to N in order to keep the fenwick, the fact is that a segment in Euler trick will always represent a subtree of depth at most length of segment since each adjacent node in the list is only one depth apart, so if you handle a fenwick in each segment tree you will end up with O(N) fenwicks totalizing a length of
in total. The fact is that each segment don't need a array from 0 to N in order to keep the fenwick, the fact is that a segment in Euler trick will always represent a subtree of depth at most length of segment since each adjacent node in the list is only one depth apart, so if you handle a fenwick in each segment tree you will end up with O(N) fenwicks totalizing a length of  using a vector or a simple array for each of size
using a vector or a simple array for each of size 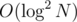 that will act nearly as a
that will act nearly as a  due to the fenwick being too small and we know actually fenwick is also below
due to the fenwick being too small and we know actually fenwick is also below  in random cases.
in random cases.
sizeOfSegmentand has some offset variable in each node. This way there is no constant and even more, the fenwick in the majority of the cases will be very small or completely ignored if the range of depth it convers is disjoint to the update or query. This leads to aThanks for explaining! I'm not sure how I didn't think of that. But I'm not sure if it will be on random cases. Because you will need a
on random cases. Because you will need a  for the query to find the corresponding index in the fenwick (we can binary search on the values). But still it's a really simple way to do
for the query to find the corresponding index in the fenwick (we can binary search on the values). But still it's a really simple way to do 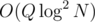 solution. Thanks again.
solution. Thanks again.
No, you can see the idea, you dont need binary search. In my sqrt(N) datastructure i find the normalized index in O(1) you can do the same here.
It's well-known in China. Someone often calls it "block tree".
I think it's just simple sqrt-decomposition.
Many thanks!!!!, any reference for that, probably translated to english :p. Oh, man you red and orange coders are amazingly full of knowledge. Also I want to know if it can be extended to or something.
or something.
can you provide a link for the complete code for it, because the link on the blog doesn't open.
100589/20273231