Hi everyone! I wan't to share some interesting fact about how we're going to challenge almost every solution, that uses polynomial hashes modulo 2^64. We'll hack any solution, regardless of it's base (!), the only thing we need, that it's using int64 with overflows — like many coders write hashing.
Keywords: Only today, only for you, ladies and gentlemen: we're gonna challenge Petr's solution in problem 7D - Palindrome Degree from Codeforces Beta Round #7!
Is it interesting? Welcome reading after the cut. Firstly, for the most impatient of you. Here's the source of the generator:
const int Q = 11;
const int N = 1 << Q;
char S[N];
for (int i = 0; i < N; i++)
S[i] = 'A' + __builtin_popcount(i) % 2;
// this function in g++ returns
// number of ones in binary representation of number i
Let's try solutions of two CFBR #7 winners on this test: Petr Mitrichev's and Vlad Epifanov's. vepifanov solution doesn't contain hashing and so, it works correct: the answer is 6. But Petr's solution returns 8. After a little bit thinking it becomes clear, that the answer on such test for this problem is always (N + 1) / 2 — Vlad is 100% correct.
Moreover, if we take Q = 20, then Vlad's solution returns correct answer 11, but Petr's one returns 2055, what is obliviously wrong :-)
I'll prove, that starting from Q = 11, there are lots of collisions in this string.
Let's look on that string. How was it formed? It's beggining like that:
ABBABAABBAABABBABAABABBAABBABAABBAABABBAABBABAABABBABAABBAABABBA...
It's true, that it can be formed by recurrent rule S -> S + (not S), starting from с S = "A", where (not S) means string after changing A на B and vice versa. Let's denote S for fixed Q like SQ.
Let's remember, what polynomial has is. It's function of string S of length l, equal to 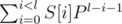 , where P is some odd number.
, where P is some odd number.
I claim that hash(S[0... (2k - 1)]) for some sufficiently small k k will be equal to hash(S[(2k)... (2k + 1 - 1)]).
That means, that for Q = 10, hash(SQ) = hash(not SQ). That's very cool, because it SQ and not SQ will appear in bigger order strings many-many times because of reccurent condition.
Let's see what does condition hash(SQ) = hash(not SQ) mean.First, we can take zeros and ones in coefficients instead of ord('A') and ord('B') — we can just take 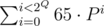 off the both parts of the equation.
off the both parts of the equation.
What is hash(not SQ) — hash(SQ)? It's simple to understand, that it's
--- it's just sign-alternating sum of P powers, where signs change by similar ABBABAAB...-rule.
Let's consequentially take factors in this expression off the brackets:
(maybe, it's multiplied on (-1), but there is no matter for it.)
Now the main thing — this value modulo 2^64 will become zero very-very fast!
Let's understand, what's the maximal power of 2 this value is divisable. Let's look on each of Q - 1 factors. (i + 1)-st factor P2i + 1 - 1 = (P2i - 1)(P2i + 1) is divisible by i-th and by some even number P2i + 1. That means that if i-th bracket is divisible by 2r, then (i + 1)-st is divisible at least on 2r + 1.
So that means that (P1 - 1)(P2 - 1)(P4 - 1)...(P2Q - 1 - 1) is divisible at least by 2·22·23·... = 2Q(Q — 1) / 2. That means, that it's enough to take Q >= 12. Congratulations, this is anti-hash test!
So because of that we have such small test length in comparsion with the modulo size 2^64. So antitest size is something of order 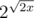 , if we use x-bit data type.
, if we use x-bit data type.
Main idea: don't use overflowing when counting hashes unless you are confident that there is no test, consisting of this ABBABAABBAABABBA... string.
How did I get that? First using of that test was in 2003 on St. Petersburg school programming contest in problem cubes (russian statements here). This problem was used in SIS) problemset. Many generations of students got WA27 on that problem, submitting hash solution. One of them was I — nobody could explain me, why is there WA for any hash base. Burunduk1 looked a bit on that test, but couldn't explain me either. Since that moment I remembered about that problem.
And now I've decided to think a bit and understand, what's happening in that test. Burunduk1 offered to post it on CF, so here it is :-)
I tried to found any information about anti-hash in web, googled a lot, but couldn't find anything. Does anybody know anything else, maybe, any papers? Maybe I'm not so good in googling?











In POI19 http://main.edu.pl/en/archive/oi/19/pre ... It also contain such a case ...
We found that case by accident during that POI :) We actually submitted a short paper about this to the next IOI journal.
Sorry to revive this, but I use a lot of hashing technique for online contests and have some questions :).
In short, the solution to not be targeted by this anti-hash test is to use a different mod (not power of 2)? For instance using mod 10^9+7. But that mod is kind of small, and with around 50k random strings it is really easy to get a collision. Using a larger mod will require to implement a function to multiply longs, and that function adds an unwanted overhead to the solution that might make it time out easily on some problems (does knows an efficient way of doing it? I can only think of a O(bits) way, where bits is the number of bits of our mod, something like this: http://pastebin.com/r5Af5zfp).
One other possibility is using two mods (that fit in an int type), and creating a pair of hash values. My question is, is that enough? I mean, enough for online contests where there won't be more than 10^8 string hashes. Through some empirical results, I couldn't find a hash collision for that, my bruteforce test code is here: http://pastebin.com/iaVp6ypH (be careful running it, it can consume pretty fast your computer memory, adjust the LIMIT variable for your purposes). Thanks!
You are talking right things. Hash value of order 10^9 + 7 can really cause collisions. But it's useful to understand why exactly collision can happen.
Imagine the problem, where you are asked to check 105 pairs of substrings of big string to be equal. Suppose that answers for each query are in fact "NO". Let's assume that due to big length hash of each substring is random uniformly distributed value over segment [0..109 + 6] not depending from hashes of other strings. Then the probability that the check suddenly gives us answer "YES" instead of "NO" is almost same with the probability of two uniformly distributed values from that segment to be equal. This probability is 10 - 9. The probability that no one of the 105 checks will fail due to collision is (1 - 10 - 9)105 ≈ 1 - 10 - 4, that is really close to 1. One the testset consisting of 100 tests the probability that you'll recieve "Accepted" is (1 - 10 - 4)100 ≈ 99%. That's pretty big probability to write such solution, so using single hash modulo 109 + 7 is ok for that type of problems.
Other type of problems involve checks like "check that hashes of 105 substrings are pairwise different". For example if we calculate number of different substrings of length 5·104 in string of length 105 and they all are in fact different. Once again, we can assume that each hash of that substrings is random uniformly distributed value from segment [0..109 + 7], that are independent one for each other. So now we need to calculate another probability: that from 105 random integers from range of length 109 no two will suddenly coincide, giving as less answer then expected an verdict "Wrong Answer".
But here appears the effect known as Birthday problem: surprisingly, but for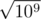 different independent randomly distributed values probability for some pair of the to be equal is about
different independent randomly distributed values probability for some pair of the to be equal is about  . So for 105 probes our probability to fail on one test will be even greater than 50%!
. So for 105 probes our probability to fail on one test will be even greater than 50%!
Here is one note: we take hash over prime modulo because for prime p Zp is a field, and for finite fields it can be proven, that all values above (that are values of random polynomials in fixed point) are very close to be really uniformly distributed over the whole field. If we take composite number, there will appear special effects like zero divisors and other, so there is needed additional analysis of probability for that cases, it can easily happen that all such calculations for them will be wrong. The main idea of my topic is exactly about surprising property of Z264, that one can easily build a polynomial of small degree (~2048), whose value is zero in any point, so it isn't suitable for solving problems with hashes.
So as you correctly said, we need to increase the hash-value space size. One way is to look on one hash modulo prime of greater size. But there is indeed a problem with their multiplication. You can multiply them with binary multiplication (such as binary exponentiation, but with adding and doubling on each step), or you can use some hacks like this (examples of code in Russian interface).
Other idea is two use a pair of hashes by two different prime modulo of order 109, let's say, p and q. Then we once again can assume that two components of that hash will be independent of each other random uniformly distributed over the Zp and Zq respectively, so in fact we have a point in 2d-space that is randomly uniformly distributed over the p·q ≈ 1018 possible values. Then in every calculation above we can replace 109 with 1018 and probability for us to fail becomes insignificant. From my experience this way is faster then previous two.
I hope this will help in understanding, when hashes can cause a collision, and why we can submit correctly proved hash solution and be sure, that it will be Accepted.
Wow, very complete response :). Thank you for the help, It definitely helped in understanding!! We should learn Russian, we miss so much interesting information only available at CF.ru posts :|
There is also a very interesting article here: http://www.mii.lt/olympiads_in_informatics/pdf/INFOL119.pdf A friend sent me, not sure if he found here on CF or somewhere else..
Look a few posts above and you will see one of the author of this article saying that they submitted a paper about this :D.
But note one other thing. Exactly as Zlobober said there are two types of problems where hashes are useful — comparing many pairs of strings and checking if all hashes are different. Note that when you just check if two hashes are equal or not, you probably won't have to check so many pairs that a probability of a collision will be high, because firstly it will rather exceed time limit than find a collision. In that case exponent in (1-p)^k (where p is a prob. of collision) grows linearly with time of execution. When you have 10^6 hashes generated modulo 10^9 number of colliding hashes will be pretty high but that doesn't change fact that if you won't do more than 10^6 queries of type "==" the probability of FINDING collision is really small (~0.999). This can be stated unless you won't do anything else than using operation "==" or "!=". But when you use other operations such as "<" the exponent and so the probability of collision may grow much faster! Best example is a simple example "are all of those hashes are different". You can sort them and check if every two consecutive values of hashes are different. But in this case you have used a specific values of hashes and that allowed you to obtain O(n^2) informations in O(n log n), so a probability of finding a collision in former example is very large.
So summing up:
I use only "==" and "!=" -> nothing to worry about
I use "<" (maybe hidden in sort or a set or a map or anything) -> use pair of hashes mod 10^9+7 and 10^9+13 or anything else.
The same in English: I came up with a workaround. Can someone break a Fibonacci hash modulo 2^32? Zlobober?
a_0 (0; 1) + a_1 (0, 1; b, 1) (0; 1) + a_2 (0, 1; b, 1) ^ 2 (0; 1) + …
Where a_i — letters in a string, b — random odd constant, ';' — delimiter in a matrix. The resulting hash is a vector of two int32's. You can compute it for substrings analogically, but you need to work with two int32's instead of one int64. Why is it a Fibonacci hash? Because one can simplify matrixes multiplication: (0, 1; b, 1) (x; y) = (y; bx + y) — this trick is used for computing Fibonacci numbers and analogical sequences.
Thanks to everyone who will try to break it!
Strings "aab" and "bba" have the same hash value.
Thank you for your example, but I guess you didn't quite understand the idea. I'll try to explain in more details. The matrix notation (0, 1; b, 1) means two by two matrix:
a_0 (0; 1) + a_1 (0, 1; b, 1) (0; 1) + a_2 (0, 1; b, 1) ^ 2 (0; 1) = a_0 (0; 1) + a_1 (1; 1) + a_2 (1; b + 1)
We can assume that char 'a' code is zero and char 'b' code is one. Then hash("aab") = (1, b + 1) and hash("bba") = (1, 2). These hash codes are obviously unequal. I guess you thought that b = 1 because of the name 'Fibonacci'. But I meant extended Fibonacci sequence when x_n = x_(n-1) * b + x_(n-2)
You are right, I misread your comment, sorry :) This approach should work, given that b > max char value.
BTW, if we consider eigenvalues of (0, 1; b, 1) it seems that your hash is equivalent to the polynomial hash with base (1+sqrt(4*b+1))/2 in the ring of numbers of the form x+y*sqrt(4*b+1) (x, y taken modulo 2^32) when 4*b+1 is non-residue modulo 2^32 (which is the case iff b is odd).
Hmm, eigenvalues interpretation is interesting.
Sorry for necroposting, but this is possible to break as well.
I will consider slightly more general construction. Let M be some 2 × 2 matrix with integer coefficients then hash of string s0s1... sn is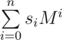 modulo 2w (w = 32 or w = 64) — also 2 × 2 matrix.
modulo 2w (w = 32 or w = 64) — also 2 × 2 matrix.
In your case,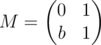 for some odd b. One can verify that M2 = M + b (b is a shorthand for bE, where E is the identity matrix) holds even in integers, let alone modulo any number (math remark: because M's characteristic polynomial is x2 - x - b). One can say that
for some odd b. One can verify that M2 = M + b (b is a shorthand for bE, where E is the identity matrix) holds even in integers, let alone modulo any number (math remark: because M's characteristic polynomial is x2 - x - b). One can say that 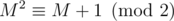 in the following sense
in the following sense 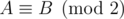 if A - B has only even entries. Therefore
if A - B has only even entries. Therefore 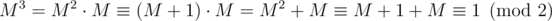 .
.
Now we can substitute M3 instead of P in the (P - 1)(P2 - 1)... (P2Q - 1 - 1) expression from the post. One can see that only important quality of P was that P - 1 and P + 1 are both divisible by 2. As shown above, in a sense this still holds for M3. Therefore (M3 - 1)(M6 - 1)... (M2Q - 1·3 - 1) is a polynomial of M with small degree, coefficients in range [ - 1, 1] and is zero on any matrix of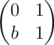 form.
form.
Even more, suppose that M is any 2 × 2 integer matrix with odd determinant (basically, nondegenerate when considered modulo 2). Then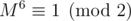 . One can verify this by brut force, but probably easier way to see this is (warning: math ahead) is noticing that nondegenerate matrices modulo 2 form a finite group of order 6 and apply [Lagrange's theorem, link is not clickable for some reason](https://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)#Applications ).
. One can verify this by brut force, but probably easier way to see this is (warning: math ahead) is noticing that nondegenerate matrices modulo 2 form a finite group of order 6 and apply [Lagrange's theorem, link is not clickable for some reason](https://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)#Applications ).
Considering matrices M that are degenerate modulo 2 may complicate things a bit, but this is not the best idea for the same reason as using even P is a really bad idea when using simple polynomial hashes modulo 2w.
Warning: more math ahead.
One can also ask what will happen if we use 3 × 3, 4 × 4 matrices, et cetera. Well, for 3 × 3 matrices and w = 64 the degree of the resulting polynomial will be 211·|GL(3, 2)| = 211·(8 - 1)·(8 - 2)·(8 - 4) = 344064 (you can read about GL(n, p) here), what is slightly more than usual constraints in string problems, but I believe that this can be hacked with more careful consideration of the same idea. And I am not sure that using 4 × 4 matrices will be faster than usual double hashing approach (did not test it though) and it doesn't sound safe either.
TL;DR: strings s and t generated by the following code should have equal Fibonacci hashes modulo 264:
This is very nice. Good observations!
In fact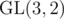 has no element of order 8 — either by bruteforce, or rational canonical form, or the observation that the (Heisenberg) subgroup of upper triangular matrices is a non-cyclic Sylow 2-subgroup, or (insert simple argument here) — so you can reduce the degree of your polynomial to 172032. I can't see how to reduce it further, since there are matrices of order 3, 4, and 7.
has no element of order 8 — either by bruteforce, or rational canonical form, or the observation that the (Heisenberg) subgroup of upper triangular matrices is a non-cyclic Sylow 2-subgroup, or (insert simple argument here) — so you can reduce the degree of your polynomial to 172032. I can't see how to reduce it further, since there are matrices of order 3, 4, and 7.
Actually the decision to use matrices seems a bit arbitrary, since multiplication is slow, and you're really only using powers of a single matrix.
We could instead use a ring of the form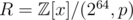 , where p is an arbitrary monic integer polynomial of degree d, say, with
, where p is an arbitrary monic integer polynomial of degree d, say, with 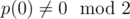 , so that x is invertible in R, and then let the hash of a be
, so that x is invertible in R, and then let the hash of a be 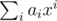 , evaluated in R. (Elements of R can be represented uniquely as
, evaluated in R. (Elements of R can be represented uniquely as 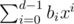 , where each bi is a long long.)
, where each bi is a long long.)
This is essentially equivalent to using d × d matrices, since any such matrix is a root of a polynomial of degree d (Cayley-Hamilton), and the minimal polynomial could be any polynomial of degree d (e.g. consider the matrix representing multiplication by x with regard to the basis 1, x, ..., xd - 1 of R).
However, each multiplication in R requires 'only' O(d2) long long operations, and each addition requires only O(d) long long additions, which is slightly better than the O(d3), O(d2) required for d × d-matrices.
For d = 4, according to my calculations the order of x modulo 2, i.e. in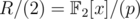 , is either 15, 7, 12, 8, or a divisor of one of them, so your hack would require a string of length 211·5·3·7·8 = 1720320, assuming you don't know p.
, is either 15, 7, 12, 8, or a divisor of one of them, so your hack would require a string of length 211·5·3·7·8 = 1720320, assuming you don't know p.
If the hacker knows the order m of x mod 2, however, they will only need length 211m. The fact that m seems to inevatibly be fairly small suggests that this approach is essentially no better than say choosing a small number m at random, dividing the string into chunks of size m, and treating each chunk as one character somehow.
Tl;dr: Just use one or more large primes.
By the way, order of any element of GL(d, 2) does not exceed 2d - 1 (simple proof here). Therefore m ≤ 2d - 1 always holds and m always is quite small.
UPD. So hacker can just generate a pair of strings with same hash for every possible "maximal" m ≤ 2d - 1 (i. e. m is a divisor of |GL(d, 2)| and does not have multiples less than 2d other than itself). Their total length won't be very big even for d = 4 and their concatenation would work as countertest in most problems.