Given 2 mutisets A and B, |A| = |B|, |A|, |B| <= 10^5, 0 <= elements in set <= 10^18. The task is to find such X that A ^ X = B or say that such X doesnt exists. How can one do that? A ^ X means foreach element of A xor it with X
→ Pay attention
Before contest
Codeforces Round 940 (Div. 2) and CodeCraft-23
38:22:33
Register now »
Codeforces Round 940 (Div. 2) and CodeCraft-23
38:22:33
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 2 | adamant | 164 |
| 4 | TheScrasse | 159 |
| 4 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/20/2024 03:12:27 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Let cnt1a be the the number of elements in A where the i-th bit is 1, cnt0a be the the number of elements in A where the i-th bit is 0. cnt1b and cnt0b are defined in the same way but for the set B. If cnt1a==cnt0b => the i-th bit in x is 1, else if cnt1a==cnt1b => the i-th bit in x is 0, else such x doesn't exist. Also in the end you have to check that x transforms set A to set B, which you can do easily with sets.
Thats not true, if cnt1a = cnt0a and cnt1b = cnt0b u cant say anything about this bit in X
In that case, first you check if x works for the btis you know for sure, and then you only care about the unknown ones. For simplicity lets just define the set C as the set containing all elements from A without the known bits. For example if we know bits 1 and 3 (0 indexed), and A={0101,1100,0011}, then C={11,10,01}. Define D the same way as C, but with the elements from B. Let Y=C[0]^D[0]. Then remove C[0] and D[0] from the set. Lets find X for this two sets. For every bit i, we have cnt1c!=cnt0c (since we removed one elemtent). cnt1c==cnt0d if the i-th bit of Y is 1 (because then we removed one 1 from one set and one 0 from another) => the i-th bit of X is also 1. cnt1c==cnt1d if the i-th bit of Y is 0 (because then we removed one 1/0 from a set and one 1/0 from another) => the i-th bit of X is also 0. Thus X=Y. Thus C[0]^D[0] = X. Thus we found a number that satisfies the condition.
Sorry if the explanation was unclear, I'm bad at explaining stuff.
Nah dude, this aint right either — look why.
If |A| is odd, theres only 1 possible X, solution from your first comment works fine. Tho theres easier way — X = (xor of all elements in A) ^ (xor of all elements in B). This is true because if u xor every element in A with some X and then u xor all elements of A u'll get A ^ X, cause |A| is odd so |A| / 2 pairs of X will just xor to 0.
Thus, if |A| is even (xor of all elements in A) should be equal to (xor of all elements in B), otherwise theres no way to do whats required. And what u were doing was like — take some random element C from A, take some random element D from B, so answer X = C ^ D, delete these elements from sets and then, magic! A ^ B = X. Got the idea? Its wrong, because this will always hold for any C, D.
You didn't get what I'm doing. I've read my solution a few times and I'm sure it's correct. Try reading again.
Btw I define the sets C and D, and take two random elements from C and D not A and B. And it works by taking any two random elements because of the special property sets C and D have (that cnt0c=cnt1c=cnt0d=cnt1d).
I mean there are cases where A = C and B = D(when for every bit theres equal amount of numbers where this bit is 1 and 0). If so u postulate that A[i] ^ B[j] is a correct answer for any i, j. How can this be true? Or is it actually?
Well, its not true. A = {4, 7, 9, 10}. B = {2, 7, 9, 12}. If u take 7 ^ 7( = 0) u obviously fail
As in the first case (in mt first comment), there wont always be a solution, and you have to check if your x works. However, if there is one solution, then any x=A[i]^B[i] will work, if they have the property I talkrd abou (proof in my second comment)
Whats wrong with these sets A, B i gave? i dont understand
There is no solution for x in the examples you gave
Oh ok then
Well i believe this is wrong — u r using fact that problem can be solved independently for bits, but it cannot. So when u fixed some 'known' bits not any pairs of elements from C, D are a correct answer anymore.
I think the problem can be reduced to the following two:
First, partition into groups by multiplicities both for A and B. Then we need to find all solutions for each group and intersect the solution sets.
For one group the problem is basically to do the same as in the original problem but for normal sets. Assume there's solution X. Then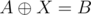 . Let's choose any
. Let's choose any 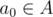 . We can write
. We can write
Now, if there is another solution X':
Then,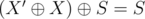 . This shows how all solutions are related.
. This shows how all solutions are related.
Yes, i think your reductions are correct, but how to solve any of them?
Can you provide a link to the problem?
Problem H from here http://codeforces.com/gym/100965/
Please send halp anyone
I'm don't check this but seems right. Look at the basis of A (name it Ba) and basis of B (name it Bb). Any of them has at most log vectors. We need to map one onto another one. If we fix image in Bb of any arbitrary vector from Ba we will now have image off whole A and we may check if latter equals B in O(nlogn) or better. Only log different images we may choose for our vector from A thus smth like O(nlog2n) we have.
What do u mean by 'basis'?
The (multi)sets are not necessarily forming linear spaces, i.e. they are not closed with respect to xor, so if you take any "basis" it may not produce exactly the set you want.
The problem is a tough one(solved by only one). You can always ask your friend who has coach rights. Judge Solution — http://ideone.com/GQJJBU
First contract the multimaps as (number,occurrences) then if the occurrences multimaps are not equal then there can't be a solution since X will map each different number to different number. Then create a candidate of solutions and try them all(random_shuffle and time cutoff seems to be the trick emplyed here).
Thanks man. I was wondering if judge's solution is deterministic or not.. well its kinda sad that its not.
Well, there exist other judge solutions which don't have time cutoff but random_shuffle just so that the solution if exists gets faster(we don't get too unlucky). So, they are deterministic. I can send you them if you need.
This was the easiest and shortest looking solution to understand so I described this one.
Well under 'deterministic' i meant smth with complexity, fitting TL, not just some random guessing
The solution you linked does not work. It almost always prints
-1in the tests generated by this code even though there always exists a unique answer.It's kostya_by's accepted solution from that gym problem link(you can re-verify if it is by using coach rights :) ). If others are interested here is Los_Angelos_Laycurse's accepted solution: http://ideone.com/WB3lgE
I just don't understand...What's the problem with solving the problem for each bit independently?
Because bits arent independ.
Oh, Now I understand...
Ok, since my last explanation was very confusing, I'll try explaining it again more clearly, also with code. We itterate on each bit i. We count how many elements in A have the bit i equal to 0 (We store this count in cnt0a), how many have it equal to 1 (store in cnt1a) and the same for B (store in cnt0b and cnt1b)
Obviously cnt0a+cnt1a=cnt0b+cnt1b=63;
Now let's assume that a solution X exists. For every bit i we must have either cnt0a==cnt1b (and obiously then cnt1a==cnt0b) (Then the i-th bit of X is 1, and transforms all 0s into 1s and viceversa), or cnt0a==cnt0b (and obiously then cnt1a==cnt1b) (Then the i-th bit of X is 0, and transforms all 0s into 0s and all 1s into 1s). Otherwise, no X exists. Then we can tell the i-th bit of X for all bits, EXCEPT for the case that cnt0a==cnt1a, then we can't tell what the i-th bit of X is. We set this bit as unknown. Let's ignore the unknown bits for now.
Next step is to find the unknown bits. Lets create two sets C and D, which contain all elemnts in A and B respectively, but with the known bits equal bits missing (or all equal to 0 for an easier code, its equivallent).
We have the following in sets C and D: cnt1a==cnt0a==cnt1b==cnt0b for every bit i, since it only contains unknown bits, which have this property, or only 0s.
Again, we assumed such an X exists. Then let's prove that X=C[1]^D[1], or any C[i]^D[j] for that matter. Let Y=C[1]^D[1]. Lets remove C[1] and D[1] for the sets entirely. Let's find X for this remaining set of n-1 elements.
Now, for each bit i, we have two cases: 1. We removes two 1s or two 0s => the i-th bit of Y is 0, cnt1a!=cnt0a, cnt1a==cnt1b, cnt0a==cnt0b. Thus, with the same reasoning as previously, the i-th bit of X is 0, and it coincides with the i-th bit of Y. 2. We removes one 1 and one 0 => the i-th bit of Y is 1, cnt1a!=cnt0a, cnt1a==cnt0b, cnt0a==cnt1b. Thus, with the same reasoning as previously, the i-th bit of X is 1, and it coincides with the i-th bit of Y.
Thus X==Y, so it works for the deleted elements too. Thus the X for sets C and D is just C[1]^D[1]. Of course, this ONLY works if there exists a valid solution for X.
Now we just sum the two Xs we've got to get the final answer.
Observe that all we've done so far was right, but we assumed that a solution X exists! What if it doesnt? Well the X we've found is the only possible X, but it might be wrong. We have to check it. It can easily be done using multisets.
I hope it was clear, if you have any questions or if I am wrong somehow please let me know.
I believe, you're code is not really correct. You're not counting the number of 0 / 1 bits correclty.
Should be replaced with
woops. Thanks for pointing it out.
I think you are wrong. As i.trofimow mentioned before, the bits are not independent. You are right that when bits are not balanced it is easy to deduce the correct bit for X. But the hardest case is when all bits are balanced. And here you are wrong that all C[i] ^ D[j] work if there exists a solution. It is true only separately for each bit level as you do prove.
Consider the hardest case, when all bits are "unknown", that is cnt1a==cnt0a==cnt1b==cnt0b for every bit i.
Your second loop then simply xors both sets with 0xffff.. and it does not matter. So let
C = D = [1, 3, 5, 10, 12, 14].
If you set i=0 and j=1, so that 1 from C maps to 3 from D, you get:
X = 1 ^ 3 = 2
and
set(C ^ X) = {1, 3, 7, 8, 12, 14} != D.
And obviously X = 0 will work. So you have a solution but not all C[i] ^ D[i] work.
Oh yeah, you are right. Thanks for pointing out my mistake.
From what I understand you prove that if a solution X exists such that if C[1] ^ X = D[1] then the solution for the remaining sets of size (n-1) would also be X. But does that help us anyway in finding a valid X? Since the assumption is C[1] ^ X = D[1]. It could be that C[1] mapping to any other D[i] leads to a valid X but not to D[1].
Any X=C[i]^D[j] works, there are multiple solutions.
No they don't. hellman_ already gave an example.
Yup, got my mistake, thanks.
where is its judge?
Problem H from here http://codeforces.com/gym/100965/
1) The answer can be broken down independently to each bit. 2) Having reduced the problem to one bit, you can easily see that the answer can be zero or one, or both (when the elements that are 1 equal the ones that are 0).
Bits are not independent though..
Yeah, never mind.
What about putting all elements of A (with multiplicity) in a binary trie, do the same with elements of B and then doing tree isomorphism?
Probably I did not understand idea completely but you need need to choose whether to swap subtrees for every vertex on the same level in the same way (because you xor all numbers with a fixed number), so this problem is not directly equivalent to tree isomorphism.
UPD. I mean, consider A = {00000, 11111} and B = {00000, 11110} (I write numbers as bit strings for clarity). Then corresponding tries are isomorphic as rooted trees, but no x such that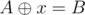 exists.
exists.
Yes, you are right, it's not exactly tree isomorphism. Now, I wonder if an adaptation of that algorithm is possible.