Hello CodeForces Community!
After a series of four ICPC regionals in India (Amritapuri, Chennai, Kharagpur, Kolkata), the top teams from the respective regionals have been shortlisted and they will now compete at the final leg of the ACM ICPC Asia India regionals — ACM ICPC India Final 2016. Over 90 top teams have geared for the Final which makes it an exciting battle to watch. My best wishes to all the teams who are competing tomorrow.
Further, I would like to invite you all to the parallel mirror contest which will be take place at ACM-ICPC Asia — India Final Onsite Mirror Contest.
For those who are preparing for the ICPC onsite regionals this would serve as an ideal platform to practice as it would simulate the real onsite contest.
Contest Details
Time: 30th December 2016 (1100 hrs) to 30th December 2016 (1600 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Contest link: https://www.codechef.com/INF16MOS
Registration: You just need to register as a Team on CodeChef. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.
Good Luck! Hope to see you participating!!
Note: The mirror contest will run in parallel to the main contest with an hour delay.










Problem B is the same as https://www.codechef.com/problems/VALMAX. And the same bruteforce solution can pass.
Constraints were N = 100000 and K = 1000. Are you sure brute force will pass? The expected solution was a not so trivial Tree DP in which you process nodes in increasing order of their tin values. Can you show the bruteforce code which passes?
P.S : I don't think the problems are similar. For the problem you linked to, your own solution is O(N2), where as today's B had an O(NK) solution.
P.P.S : I checked out your AC Code and it seems O(N * min(K2, N))) is passing. This was not intended. It is because of slightly weak test data (I am not sure what I did wrong, since I added all edge cases/ stress tests. I am not fully sure how to break your code since you're taking min of k + 1 and the current subtree size at each edge of the tree). Luckily, we got only one such hacky solution today in the actual contest in the 299th minute, by a team who was 2nd already and they remained in 2nd place, so there was no net affect in the RankList! The other accepted ones were optimal solutions.
Can you elaborate on your tree dp idea? Couldnt come up with anything better than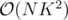
Sure.
First lets' compute tin and tout for each node by doing a DFS.
Our DP State will be DP[x][i] = Best i sized subset we can make using all nodes y which satisfy :
We're looking for DP[CEO][K].
When we're at node x, we'll make a copy of the DP array we already have and pass it by reference to its children. Then we can merge the childrens' answers with x's answer because for each size k, we have only two options :-
We take maximum of both options. Its' a bit weird to explain, but this code should make things clear.
Clever :)
NibNalin showed me a more understandable way to explain the same solution. Here is the idea :
So we find the tin and tout values of the nodes. Let order[x] denote the node y such that tin[y] = x. Our DP state is DP[i][x] denotes the best x sized subset we can make using all nodes having tin values in the range [i, n]. To compute DP[i][x], we have two options :-
1) We do not take order[i]. DP[i][x] = DP[i + 1][x]
2) We take order[i]. DP[i][x] = DP[tout[order[i]] + 1][x - 1] + val[order[i]]
Take maximum of both. It is easy to see that this does not violate any of the constraints.
How to solve C? And does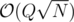 pass in E or is there a better solution?
pass in E or is there a better solution?
I solved E with an nlogn solution where n = r+g. I found for each frog the starting time when it would enter [a,b] and the finishing time when it would exit [a,b]. Sort all important timestamps and find the answer.
Oh sorry wromg problem I meant H and not E
I did parallel binary search. You can see this technique here. To apply it here, we just have to add the strings to a trie one at a time, reset the trie if neccesary. You can check the offense count of each employee by traversing the trie for each word the employee say.
Code
I was the setter of this problem. There are various ways to solve this problem. My solution uses parallel binary search along with a trie and BIT for range updates. But this is an overkill and easier solutions exist. For example, you can use a persistent trie and normal binary search. There are even simpler solutions too but as I am not sure about them, I won't go into those.
Another solution put forward by Baba. For each node in the trie, store in a vector the indices of the swear words ending there. Then for each query set, perform a binary search. To validate the 'mid', traverse the trie using the strings of the query set and in each node you visit, perform another binary search (eg. lower_bound()) to get the number of swear words ending at that node whose index <= 'mid'. Complexity is O(n*logn*logn).
If you are interested, you can find my code here.
easier solutions exist. For example, you can use a persistent trieCould you please explain the persistent trie + binary search approach in a little more detail?
Note that if you insert a string S into a trie, then it changes |S| nodes (always including head).
So you can store for each i from 1 to N a trie made using the employees words 1... i using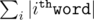 memory and time (see here for some idea on how to implement persistent data structure).
memory and time (see here for some idea on how to implement persistent data structure).
Finally, for each query, to evaluate binary search predicate, run through each word in the query, and check how many words in trie are prefix of this.
You can show that this takes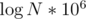 (because sum of length of all strings is ≤ 106.
(because sum of length of all strings is ≤ 106.
How to solve J? I tried thinking about a solution but gave up very quickly because it felt like anything I thought would be too messy to implement.
Also, what is intended solution for C?
I made it pass by observing that the matrix of dot products had a special form in the sample test. I assumed that it would hold for all n and came up with a way to incrementally construct my solution by placing first point at (1,0,0,...,0). Then fix first co-ordinate for remaining points by my dot product observation. Then rotate remaining points s.t. 2nd point has co-ordinates (x,y,0,0,0,..,0). I know x and therefore can find y since point lies on unit circle. Keep repeating till we have our entire set.
I think the answer for C is an n dimensional regular simplex
I formulated a recurrence. It used the fact that you can add the new point in a direction perpendicular to the plane formed by the previous points, to get the solution for the higher dimension. Other than that there were uses of Pythagoras theorem. The complete solution would be a bit difficult to explain without figure.
I solved the problem in the following way. First, imagine a vector from the origin to each point. Let's first find the angle between every pair of vectors (these should all be the same).
I'll give the explanation for this concerning 2D, but it can be extrapolated to any dimension. For 2D, consider the plane x+y+z = 0, This is in 3D, but a 2-dimensional hyperplane. Consider the points (1,1,-2), (1,-2,1), (-2,1,1) in this hyperplane. We note that they are the same distance from the origin, and are also equidistant from one another. To find the angle between two vectors, we have dot product formula involving cosine of the angle. In this manner we proceed for any dimension. The points (1,1,.,-n),(1,1,..,-n,1)...(-n,1,1,1...1,) are the points we consider.
So, we have found the angle, but we cannot use these coordinates for our answer since they are in wrong dimension.
Say we already have the solution for dimension n-1, Let's find solution for n. Our current points are in dimension n-1, For now, add a coordinate of 0 in the n-th dimension for each point. This creates a hyperplane as well. We must add another point to have a total of n+1 points. We will make it perpendicular to the hyperplane we have created. So the point will be (0,0,...,1). Now we have a total of n+1 points, but the angle is incorrect.
We currently have a 90 degree angle from the last point vector (0,0,...,1) to every other one. Say the angle we calculated is theta. We need to rotate each of the first n vectors by theta — 90 degrees. (It is guaranteed that theta > 90 by the way — this is not something you need to prove, you can print values and see it's true).
Now, to rotate by x = theta-90. It is easy to think about this going from 1D to 2D. You can easily work it out on your own. Remember we have a 0 in the last coordinate of each point. Make this equal to -sin(x) and multiply every other coordinate by cos(x). (you can convince yourselves this is true for the 1D to 2D example. This same idea holds for all other).
We have way of going from n-1 dimensions to n dimensions. Base case is 1D, where solution is -1; 1. Therefore we are done.
My Solution
Can someone explain the solution for A please?
More specifically, How do I do modular calculations on a/b where a%m=b%m=0 and how do I find the factorial without TLE?
You can break factorials mod m into chunks of size m - 1, skipping all multiples of m. Now observe how all chunks except the last one teudce to (m - 1)!
Ok, so if we have to calculate (17!)/(13!) mod 11, it basically reduces to:
(10! * 6!)/(2!). And now to calculate final answer, we just have to do regular modular operations right?
Yes
Any hints for Problem D — Pinocchio