I noticed that almost all of the programming blog shared O(n*(log n)^2) implementation for suffix array construction.
I saw O(n * log n) implementation in the book "Competitive Programming 3" — by Steven & Felix Halim. But it seems hard to understand and needs more time to code, since the code is longer compared to the O(n * log^2 n) implementation.
Besides, O(n*(log n)^2) implementation is easy to code and easy to understand.
So, my question is: Is it good enough to learn only n(log n)^2 suffix array implementation for solving problems related to suffix array in any contests? Have you seen any problem where O(n*(log n)^2) fails but O(n*(log n)) passes?
If you think that one must know O(n*(log n)) implementation, can you please share any easy to understand and comparably short code for O(n*(log n)) implementation?
Another question: any problem which is solvable by suffix tree, can be solved suffix array? If so, can we skip suffix tree and always use suffix array?
Thanks in advance.











As far as I remember there are some questions which requires you to actually walk and work in the tree, so suffix array does not always work :(
Example: https://www.hackerrank.com/contests/worldcupfinals/challenges/str-game
Just replace the regular sort with counting sort, this should improve the complexity to NlogN
Would you please share a code to construct suffix array in nlogn using counting sort? This will be very helpful for me.
You can find it on e-maxx in the middle of the wall of text. However, it's quite bad, as all the codes on that website.
It's my $$$\mathcal O(n\log n)$$$ suffix array with radix_sort:74925146
Have you seen any problem with decent TL? ... Yes, I have. It's better to just have a prewritten .
.
If I have to manually code a suffix array I write the O(N (log N)2) version.
But if prewritten code can be used, then I use the code for the LCP-Table wrapped around the O(N) implementation from here (publication).
Some problems require an on-line construction, which afaik makes the use of suffix-trees necessary.
Some time ago I compared two implementations on Timus 1393 problem ... and O(Nlog2N) worked two times faster! Since then I totally abandoned O(NlogN) approach. If somebody can beat my current time with it — please let me know, maybe I'll reconsider.
After reading some of your posts such as Efficient Segment tree, Fast and Furious IO... it's clear that you have a gift for implementation. It would be great if you start some implementation blogs, something like https://sites.google.com/site/indy256/algo/ . I am sure that you will have a huge number of followers :))
Could you share your implementation?
STL sort is very fast and I have examples of some tasks (not including SA) when replacing counting sort with STL sort (which makes complexity worse) actually improved the runtime. If TL is strict then improving that approach to n log n will probably have little significance (if any) and it is better to have O(n) prewritten.
Deemo used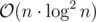 Suffix array and got accepted in IndiaHacks 2016 — Online Edition (Div. 1 + Div. 2), 16814760.
Suffix array and got accepted in IndiaHacks 2016 — Online Edition (Div. 1 + Div. 2), 16814760.
Very late but can you share where you may have learned about olog^2 n SA? I see it at geeks for geeks https://www.geeksforgeeks.org/suffix-array-set-2-a-nlognlogn-algorithm/
The problem is a lot of people in the comments claim to have bugs... I'm not sure though.
Pro tip: Never trust any code on geeksforgeeks. I made that mistake twice and both times I got burned so bad. In one case they claimed it was N^2 but I read the code and it was actually N^3 (systest seemed to agree with me). Luckily, it was only in upsolving.
There's an ancient stanford pdf with correct code, use that one instead.
This is pretty much everything you need to know to code SA in nlog^2(n)