8VC Venture Cup 2017 — Elimination Round[Editorial]
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3640 |
| 2 | Benq | 3593 |
| 3 | tourist | 3572 |
| 4 | orzdevinwang | 3561 |
| 5 | cnnfls_csy | 3539 |
| 6 | ecnerwala | 3534 |
| 7 | Radewoosh | 3532 |
| 8 | gyh20 | 3447 |
| 9 | Rebelz | 3409 |
| 10 | Geothermal | 3408 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
| Name |
|---|



I don't understand E, can you elaborate on why this works?
Answer is possible only for K = 2 or 3. There are two construction algorithms. For K = 2 one path works. For K = 3 idea is a bit more complex.
Thanks for someone hacking my D solution..
I am jealous... :'(
In C, I solved it slightly differently. For any vertice x whose diameter ends in y, clearly the vertice y has a diameter that ends in x (so v[x]=y and v[y]=x). Simply check for all vertices the ones that cycle back onto themselves, (i.e. v[v[i]]==i), and the number of such distinct elements is the answer.
3855373
There is some alternative solution in D without any structures. Look at this! http://codeforces.com/contest/755/submission/23862072
could you explain a little ?!
With each round we cross on a diagonal more. However, as an exception at the beginning of the circle only one more. At the moment, I can not rigorously prove.))
I solved D without segment tree, with complexity O(n)... Here is the code
Me too. It's a simpler idea.
can you please elaborate your idea? why did you increase cycle for 2nd time? thanks
It can be easily visualized by drawing a polygon by hand.
In the initial round around the polygon going from 1 to n, the diagonals will not intersect. So every diagonal will produce 1 extra section. The final diagonal around which cross the point 1 will produce +2 sections because it will intersect the diagonal which starts at point 1 to (k+1). Every subsequent diagonal will intersect with two other diagonals (one starting from a point before their starting point and one between the starting and ending point) producing +3 sections each time. Suppose x sections were introduced with every diagonal. The final diagonal which crosses point 1 will introduce x+1 sections. And every subsequent diagonal in the next round will produce x+2 sections. Complexity: O(n) because every point becomes a starting point for a diagonal exactly once.
And of course, setting $$$k$$$=min($$$k$$$, $$$n-k$$$) is imperative here.
System judged my A solution in 15 minutes and it gave WA test case #2 because of stupid mistake! Then I corrected my mistake less than 1 minute and got AC. But I send my first solution in 2nd minute, and after correcting mistake in 17th minute. I lost points for nothing! I know this happened not just me, but Codeforces team please don't make mistakes like that.
Nice problemset. Loved the first problem.
Could someone explain the tutorial for D? I find it a little difficult to understand.
Why on solution problem D: k = min(k, n - k)?
As you should just consider the number of diagonals connecting the vectices on the minor side instead of the major side.
If you do not get n-k as k if n-k is smaller than k, you will calculate the number of diagonals connecting the vertices on the major side, which is incorrect.
Can you explain this thing more elaborately? I am unable to prove it.
Try to draw by hands what happens with 7 4
Why are n-k and n coprimes when k and n are also coprimes?
Lets assume the opposite: if
n-kandnare not coprime, then there exists some common divisord > 1withn - k = d * xandn = d * yfor somexandy. But then it follows:k = n - (n - k) = d * y - d * x = d * (y - x). So alsokis dividable byd. But thenkandncannot be coprime, because both are a multiple ofd.because (a,b) = (a — b , b)
I got it, thanks!
Problem C i used disjoin set
Yes, it can be solved by a lot of things. I used dfs to solve
I used simple DFS. Someone used DSU
So fast, nice contest tho :D
Am I the only one who has solved C by counting the number of connected components? link: this submission
can anyone explain D for me? why i got Time Limit? http://codeforces.com/contest/755/submission/23867206
Set k = 106 - 2 and n = 106. Then find your code complexity.. And assume O(109) will pass in 1 second. :)
Better set k=10^6-1 as gcd(n,k)=1 but for your case it will be 2. :)
You can test 16 B please?
Has anybody solved optimized knapsack for problem F in a different way? The author's solution is hard to understand.
you can break frequency into binary and then do normal knapsack , number of elements are now about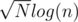 . code .
. code .
Number of elements is at most now. To see this, we first observe that number of elements is about
now. To see this, we first observe that number of elements is about 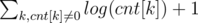 . Number of k, such that cnt[k] ≥ 1, is at most
. Number of k, such that cnt[k] ≥ 1, is at most 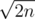 . Number of k, such that cnt[k] ≥ 2k, is at most
. Number of k, such that cnt[k] ≥ 2k, is at most 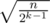 . So,
. So, 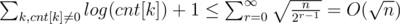 .
.
I'm having trouble to: 1) understand the following passage; and 2) assuming it is correct, how to apply it to the final inequality.
"Number of k, such that cnt[k] ≥ 2k, is at most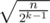 ."
."
Would you please explain it in more details? Also, would you please give the intuition behind this bound? Is it something like: Suppose you have k different cycle lengths and this k is maximum. Then k is around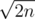 . Also, k being maximum implies that each cycle length occurs with frequency around 1. If these frequencies start to increase, then k becomes smaller than
. Also, k being maximum implies that each cycle length occurs with frequency around 1. If these frequencies start to increase, then k becomes smaller than 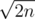 enough to compensate these repetitions and the overall sum stays around
enough to compensate these repetitions and the overall sum stays around  . Is that it?
. Is that it?
Of course, intuition behind the argument is like you have described.
Assume, that cnt[k1] ≥ m, ..., cnt[kl] ≥ m. Then the sum of lengths of cycles is at least k1cnt[k1] + ... + klcnt[kl] ≥ m(k1 + ... + kl). Since ki are all different, k1 + ... + kl ≥ l(l + 1) / 2. So, the sum of lengths of cycles is at least ml(l + 1) / 2, so .
.
Now,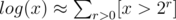 , where [x > 2r] equals 1, if x > 2r, and 0 otherwise. So,
, where [x > 2r] equals 1, if x > 2r, and 0 otherwise. So, 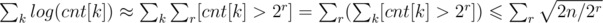 .
.
Anyway, solution described below by egor_bb has obviously operations with bitset and is not harder to implement.
operations with bitset and is not harder to implement.
Thank you very much!
Another solution is similar to binary.
The goal is to leave no more than 2 items of each weight. Then we'll have items and solve knapsack either in a simple way or with bitset.
items and solve knapsack either in a simple way or with bitset.
We can notice that for each weight in optimal answer we'll take either odd or even number of items. Let's fix weight w. We can leave one item of this weight and merge other items in pairs. If number of items with weight w was even — we'll have 2 items left, if odd — 1 item. Also now we have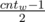 more items with weight 2w.
more items with weight 2w.
Easy way of implementing it is to iterate from small weights to big and perform merging.
After this reduction, only items remain to be considered by the usual knapsack. This follows by the same arguments pointed by ershov.stanislav in the comments above, am I right?
items remain to be considered by the usual knapsack. This follows by the same arguments pointed by ershov.stanislav in the comments above, am I right?
It is a popular idea that if you have a set of numbers with fixed sum S then there is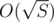 different values in set. Easy proof is following:
different values in set. Easy proof is following:
When is sum of k different positive numbers minimal? When these numbers are from 1 to k.
An interesting case of applying this idea is a set of strings with fixed total length. Since there are at most around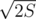 different lengths, often handling all strings with the same length in some simple way is enough.
different lengths, often handling all strings with the same length in some simple way is enough.
Yes, that is a valid argument, but only before the reduction you applied. We need another argument to prove that the total number of items remains after the reduction you proposed. And as you break the frequencies in halves, I think that the arguments above also apply to your reduction! It'd be great if someone could confirm that.
after the reduction you proposed. And as you break the frequencies in halves, I think that the arguments above also apply to your reduction! It'd be great if someone could confirm that.
After the whole process of reduction we have no more than 2 items of each weight. Thus, total number of items is no more than 2 times "number of different weights" which is
That argument is not valid, because your algorithm creates some new weights that possibly didn't exist before. Here:
And it will continue to do that until the frequencies cannot be halved anymore. So there's a possibility that for each weight w, you'll create around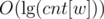 new weights.
new weights.
So we still need additional arguments to prove that, despite some new weights are created, the total number of items remains .
.
C'mon, sum remains the same all the time and it's enough. You can apply the proof at any moment. Read the explanation of algorithm again, please.
I believe that your misunderstanding is small enough to stop the conversation here and continue it in private messages.
Yes, I do believe in the bound! I'm just trying to point the exact proof for your version! I'm not trying to contradict you.
bound! I'm just trying to point the exact proof for your version! I'm not trying to contradict you.
UPD: Okay, got it! This last comment is enough: the sum will remain the same all the time, so the bound is valid all the time!
bound is valid all the time!
UPD2: And I believe that others could learn from someone else's mistakes... So it's okay and desirable to keep the conversation here. But now I got the proof, anyway. Thanks!
Problem D can be solved in O(n). http://ideone.com/gm3MCV
Auto comment: topic has been updated by kpw29 (previous revision, new revision, compare).
23858332
Can someone explain why this implementation of C gives TLE? I made each tree a set, and every time there was another element, I scanned through all the sets to see which tree/set the element would go in. Thought it was N^2.
you just need to find the connected components .
My 23855084 using UnionFind passed for Problem C. If you see
p[i] = jsimplyunion(i, j)and in the end count number of disjoint sets.Could please someone explain how to understand the following in the text of the problem G : no two balls shall occur in one group,but in the first test case they say that groups are divided in such order (1),(2),(3);(1,2),(2,3) etc.So as i can see here the ball number 2 is encountered 2 times,so i consider,that the first line(when divided in 1 group is 1 case, so the ball number 2 shouldn't be in any other groups(when divided in 1+ groups),but then i see the second line when i can see ball 2 one more time(more than 1 time,actually , but nevertheless),so as i see there is a contradiction and I can't solve it by myself,could anybody help me to understand that.I'm baffled:(
For problem E: "It's easy to see that ShortestPath(1, 4) is exactly 3. Also, ShortestPath(1, 4) in the complement graph is 3." 1 — 2 2 — 3 3 — 4
Why is Shortest Path in complement graph 3? Isn't there the edge 1-4 in the complement graph?
Also thinking about the same thing, don't mind me just leave a comment here to get notifications if someone answer it
The longest shortest path in complement graph is for (2,3) of length 3(2->4->1->3).The problem doesn't require the two pairs of vertices to be same in both the graphs.
Can someone please look at my submission in C and help me in finding out what went wrong. http://codeforces.com/contest/755/submission/23858330 Thanks in advance.
consider the following forest: 2-1-3-4. Then the input would be 4 4 2 2. running your code outputs 2 when it should output 1.
Okay. Thanks a lot!
23875480 My O(n) submission from problem D in python3 is giving TLE EDIT: It works in C++
The reason is that you made multiple print out. As far as I know, it is better to declare a String variable output and keep updating that, subsequently only call print() once at the end of the program.
My Java code took almost 3s to run problem D because of the same reason. When I changed to a StringBuilder to maintain the output, the runtime reduced to only 0.3s.
I am trying this, but it isn't helping :(
23882430
There's surely a typo in the editorial from problem E. If the shortest path between two vertices in a graph is more than 1, then the shortest path between the same two in the complement graph must be exactly 1. Please correct.
Why, one of the graphs should contain an edge between them bcs two of them concatened should make fully connected graph.
Problem C does not require implementing dfs, but knowledge of dfs. It can proven that each node in the tree has the farthest node which will be one of the two ends(nodes with farthest distance between them).There can be more than one node at one of the end but here it is fixed(with the smallest id).We can map the values which corresponding to either of these ends. Total elements in the map will be our answer.
I tried to implement authors approach in Problem F but I am getting TLE on test 6. I have tried taking T as 100 and 200.This is my approach :http://codeforces.com/contest/755/submission/23886931
Can someone explain why in problem E, k=1 is not achievable if I just add one red edge?
Because the graph won't be connected.
got it, thanks
Looks like odd.
cf: http://codeforces.com/contest/755/submission/23902417
Oops, duplicate of http://codeforces.com/blog/entry/49793?#comment-337788 . (Sorry. please don't downvote this...)
For test case #8 of E, I don't see why does the judge's answer produces k=3, shouldn't the white subgraph has a diameter of 2?
In solution for problem F it's somewhat arbitrary to split numbers that way (smaller than T, larger than T).
Let's analyze, for some number x:
We can see that complexities don't depend on x at all, but only on its frequency fx. So what makes most sense is to use first algorithm for numbers x such that fx < B and second algorithm for other numbers.
Splitting them in a way proposed in editorial is still good heuristics, since we can expect smaller numbers to have larger frequency.
Another way to solve problem G.
It's easy to see after after getting dp equations and interpreting each row of the dynamic as a polinomial the following result: Pn + 2 = (x + 1) * Pn + 1 + x * Pn
At the begining one approach inmediatly came into my mind (matrix exponentiation). But i was computing too many fft and it was TLE :(
Another way to tackle this equation is solving the linear homogeneous equation related. Notice that the coefficients of this equations are polynomials.
Z2 = (x + 1) * Z + x
Z2 - (x + 1) * Z - x = 0
The form of the formula is:
Pn = A * Z1n + B * Z2n
P0 = A + B = 1
P1 = A * Z1 + B * Z2 = x + 1
Solving this system to find A and B we get:
B = P0 - A
Now we only need to figure out how to compute inverse and square root of polynomials. Using the technique described by vfleaking here we can do both things with total complexity .
.
The final complexity is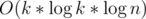 because we need to do fast exponentiation to find the answer in
because we need to do fast exponentiation to find the answer in 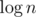 steps.
steps.
Solution here.
A much simpler solution: Use matrix exponentiation to compute $$$P_n$$$, just like Fibonacci numbers. Remember to take the polynomials modulo $$$x^{k+1}$$$ after each operation. Surprisingly, in my case it only took around 20 lines of code, excluding the templates (polynomials, matrices, modular arithmetic).
I tried to implement FFT for problem G but somehow the FFT function went wrong, I tested the function under the circumstances [MAXN = 16, logMAXN = 4, n = 4], and the FFT result of the array is very odd. The imaginary part has incorrect positive/negative sign, and the real part output zig-zagged along the array. Can someone please help to point out where did I made a mistake?
Code: http://ideone.com/tUoCwO
The expected and actual output is also included
Thanks in advance. :)
Tee-hee, I got O(k2) to pass on Problem G after the contest.
In problem E, which sentence said that both red and white subgraphs need to cover all the n vertices?