Given N distinct integers from 1 to N, you have to find the number of ways the N integers can be rearranged in M empty slots such that, no integer matches with its slot index. Note that, slots are indexed from 1 to M.
Print the number of ways modulo 23377788.
0<=N<=M<100000 and It has 200 test cases.
I came up with a solution like this but not sure its correct or not. And have not any idea to modulu it by non prime. 











Modulo operations like addition/multiplication are done the same way as in primes. For modulo inverse, you must be careful. Note that if the number you want to find the inverse is not coprime with the mod, then there is no solution. Otherwise just calculate this number raised to the (phi(mod) — 1) power, this follows from euler's theorem.
Also, extended Euclidean algorithm can be used be calculate inverse.
For n ≤ M we have M - 1 variants, for n > M we have M variants. You just need two involutions by modulo and operation like ab % MOD.
A little bit explanation please.
Lets consider arbitrary number n. We have only one restriction: n cannot be matched with n-th box. From the statement we know that number of boxes greater or equal to any n, thus number of ways to correctly put n to some box is M - 1 (we may put n to any box except n-th box). Total number of rearrangments is (M - 1)N % MOD. All you need is multiplying two numbers by modulo.
You can use in Codeforces.
in Codeforces.
\frac{N!}{(M-N)!}\times \sum_{i=0}^N (-1)^i\frac{(M-i)!}{i!(N-i)!}Add dollar sign in both sides.I think you can use Chinese remainder theorem to solve your problem.
While it doesn't answer the general question, you can read more about derangements (permutations where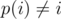 ) here:
) here:
https://en.wikipedia.org/wiki/Derangement