Hello Codeforces, I hope you enjoyed the round!
Just some notes about the problems:
In problem A, the picture and example notes should complete your understanding for the problem if the statement itself is not clear.
Solutions that check the lights of each part separately should have failed on pretests. My bad.
Problem C was assigned as B at the beginning, but moved to C lest it is harder than B difficulty. However, I think problem B is still easier than problem C (check the solution below).
I thought problem D is easier than problem E. Once, conditions are well-understood and related to each other and the problem is modeled correctly, then its implementation is easy.
The points I have just described is my own opinion in the problems. Of course, you might have a different point of view. However, I would like you to keep in mind that I did my best to make statements clear and pretests strong.
Thanks for your understanding!
812A - Sagheer and Crossroads
For pedestrian crossing i (1 ≤ i ≤ 4), lanes li, si, ri, si + 2, li + 1, ri - 1 are the only lanes that can cross it. So, we have to check that either pi = 0 or all mentioned lanes are 0.
Complexity: O(1)
812B - Sagheer, the Hausmeister
When Sagheer reaches a floor for the first time, he will be standing at either left or right stairs. If he is standing at the left stairs, then he will go to the rightmost room with lights on. If he is standing at the right stairs, then he will go to the leftmost room with lights on. Next, he will either take the left stairs or the right stairs to go to the next floor. We will brute force on the choice of the stairs at each floor. Note that Sagheer doesn’t have to go to the last floor, so he will go to the highest floor that has a room with lights on.
Complexity: O(n·2n)
812C - Sagheer and Nubian Market
If Sagheer can buy k items, then he can also buy less than k items because they will be within his budget. If he can’t buy k items, then can’t also buy more than k items because they will exceed his budget. So, we can apply binary search to find the best value for k. For each value k, we will compute the new prices, sort them and pick the minimum k prices to find the best minimum cost for k items.
Complexity: 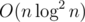
812D - Sagheer and Kindergarten
Let’s go through scenario requests one by one. For request a b, if toy b is free, then child a can take it. Otherwise, child a will wait until the last child c who requested toy b finishes playing. Since, no child can wait for two toys at the same time, each child depends on at most one other child. So we can put an edge from the a to c. Thus, we can model the scenario as a forest (set of rooted trees) as each node has at most one outgoing edge (to its parent).
For query x y, if toy y is free, then child x can take it and no child will cry. Otherwise, toy y is held by another child. Lets denote z to be the last child who requested toy y. So x now depends on z. If z is in the subtree of x, then all children in the subtree of x will cry. Otherwise, no child will cry. We can check that a node is in the subtree of another node using euler walk (tin and tout) with preprocessing in O(n) and query time O(1)
Complexity: O(k + n + q)
812E - Sagheer and Apple Tree
In the standard nim game, we xor the values of all piles, and if the xor value is 0, then the first player loses. Otherwise, he has a winning strategy. One variant of the nim game has an extra move that allows players to add positive number of stones to a single pile (given some conditions to make the game finite). The solution for this variant is similar to the standard nim game because this extra move will be used by the winning player, and whenever the losing player does it, the winning player can cancel it by throwing away these added stones.
This problem can be modeled as the mentioned variant. Lets color leaf nodes with blue. The parent of a blue node is red and the parent of a red node is blue (that’s why all paths from root to leaves must have the same parity). Blue nodes are our piles while red nodes allow discarding apples or increasing piles.
If the xor value of blue nodes s = 0, then Soliman loses on the initial tree. To keep this state after the swap, Sagheer can:
swap any two blue nodes or any two red nodes.
swap a blue node with a red node if they have the same number of apples.
If the xor value of blue nodes s ≠ 0, then Sagheer loses on the initial tree. To flip this state after the swap, Sagheer must swap a blue node u with a red node v such that 
Complexity: O(n + maxA) where maxA is the maximum value for apples in a single node.
You can read more about games from this link










Very interesting E problem.
can someone give me a good game theory reference in english?
use yandex translate
And where can i found all about XOR (and bits)? I've seen that it solves some math problems like "nim", But I never have found a good resources about all its features and properties
I can't think about features of XORing. This article has the cleverest usage I found about it so far. For bit manipulation in general, check topcoder tutorial: A bit of fun with bits.
This website is awesome, but written all in Russian. It helped me a lot learning new topics as game theory. I used yandex translate together with google translate. Sometimes it sucks but better than many other resources. So, my advice for you is serious.
Hey,
Is there anyway to solve without the condition that parity is same(Just to find whether the tree is winning or losing position in general tree )?
No idea actually :)
see the link given at the end of editorial .
Check out John Conway's book — Winning Way for your Mathematical Plays
I still cannot grasp the problem C. Is not it a standard knapsack DP problem?
DP will not pass time/memory limits. Just a simple binary search solution is enough.
It can't be solved with knapsack because the costs we use to find the optimal solution depends on the optimal solution itself.
edit: nvm I see this case is invalid
Problem D is too hard to understand. At first sight I think it is something about DAG, which is too difficult for Div. 2. When I finally get the author's idea, there is no time for me to implement :(
I thought it's about finding the number of nodes in all the paths going from x to y in a DAG. Now I'm reading the editorial and can't find anything similar :D
Same here! During the contest I modeled it as the number of nodes that become part of a cycle when an edge is added to a DAG. Couldn't think of a reasonable algorithm for it.
Same +1. This is "finding the intersection of u's descendants and v's ancestors in a DAG," which of course has no efficient solution.
(I don't blame the statement for this, it's my own carelessness not to realize this supposedly obvious fact. The statement is clear to me though it would be great just to make it shorter.)
Yup I thought this is what we want to find too...........
I thought the conditions are clear. If you will put a dependency edge from one child to another, then the condition "No child can request a toy while waiting for another" should make it clear that each child has at most one outgoing edge. Thus, it is a tree not a DAG.
Sorry if this sounds rude or harsh. But if there are 4 comments all with positive upvote about how unclear the statement is, then the statement is probably unclear. Furthermore, only 1 yellow of out so many yellow and red solve it out of contest, which suggests most of them misunderstood it. I am not saying what you mention is not in the statement, but what you should take away is that the presentation is not clear, and therefore should do better next time by either putting such case in the sample task, or simply making it easier to understand.
I have solved question B, using DP time complexity O(n*m) Solution B
Your complexity is n*m.
You need n*m operations to read, and n operations to solve dp.
Then the correct time complexity is O(n*m)
Yes, this is true. However, brute force should be always the easier solution. Your solution is nice for larger constraints.
your dp looks a kind of complicated in fact. here is a ezier scenario 27518902
I think mine is more readable :)
For each floor save max distance from left and right side to switch off all the lights (
l[n]andr[n]in code). Then choose for left: go from lower floor left side and go to max light and then return back (it will take us(l[i] + l[i]) + 1minutes on current floor) OR go from lower floor right side (it is constantly(m + 1) + 1minutes). Do not forget+ 1needs to go upstairs.The same for right. And also check if last
cntfloors hasn't lights at all (then we could get answer not from last ([n]) floor, but from[n - cnt]).http://codeforces.com/contest/812/submission/27523909
Problem B has a dynamic programming solution. Complexity: O(n.m) 27496654
I have a somewhat simpler solution of E.
The game described is a variation of staircase nim, in which only odd numbered positions are important for computing the nim-sum. Its different because in staircase nim, the coins(Apples) in the last step, are not removed. But it can be handled by adding one empty node to each leaf-node.
By careful observation, it can be seen that in trees with even parity paths , even-positions are important and in odd-parity paths, odd positions are important.
We can compute the nim-sum of the tree by this, and the rest is similar to editorial. (Blue nodes are important nodes).
Solution
I think your solution is the same.
Problem B -- How to solve if we remove "he will not go upstairs until all lights in the floor he is standing at are off" condition?
won't that be just travelling salesman problem ?! Solvable using DP with bit mask in O(n * 2^n)
Not exactly, there might be more than n lights and you may enter each floor from any side, so the mask can't be simply the floors, it should be the lights. I think there's an O(n) dp where you make a mask of the ways you need to use (down on left/right, got here from left/right) but it looks tricky (at least without trying to code it and just thinking).
oh, yes. my bad. The n in my comment represents the number of lights not floors. Which is a much worse complexity.
Consider the state (floor, stairs, mustLeft, mustRight):
floor indicates the index of the current floor (we will start from ground).
stairs is a binary number: 0 for left stairs and 1 for right stairs.
mustLeft is a flag. If it is 1, that means we must reach the left stairs by passing through the whole corridor in the current floor, or by moving downstairs later from the upper floors. It is set to 1 if the left stairs of lower floors must be reached to reach some rooms with lights on (this is explained in the next paragraph).
mustright is a flag similar to mustLeft but for right stairs.
Assume we have a state (floor, 0, mustLeft, mustRight). Now, we have two options:
pass through the whole corridor to the right stairs and go to state (floor + 1, 1, 0, 0).
pass to a certain room r and go back to left stairs and go to state (floor + 1, 0, 0, newMustRight). newMustRight is 1 if and only if there is an unvisited room after r with lights on or mustRight = 1. Let q be the first room after r with lights on. We will hypothetically assume that we are standing at both left and right stairs. So, we will go left -> r -> left and right -> q -> right. And we set mustRight = 1 for the next state to inform it that the right stairs must be reached anyways to take it downstairs to the current floor and our hypothesis becomes valid.
The dp value of the current state is equal to the dp value of the next state plus:
And do the same for stairs = 1.
What remains is handling where we will end this path. This can be handled with an extra flag indicating if we decided where to stop or not. If we are to choose a room to stop at (r or q of a certain floor), we will remove one "back" calculation as we don't have to go back to stairs. One another modification is that mustLeft and mustRight will take three values 0, 1 and 2. The default value is 2, because the stairs, we will take downstairs to reach q needs to be taken again upstairs. Unless it is set this for the end room in which case it will take the value 1.
The complexity is O(nm).
It's an interesting question and I hope my solution is correct. Let me know if you need further clarification.
I not understand problem D, very complicated description.
Can anyone explain dp solution for B . I am trying brute force but there are many small complications so its better to solve via dp . Btw I am a beginner to dp so please try to explain as simply as possible . Thanx
since there are n #rows, so a dp state will be defined as dp[i][j], where j={0,1} and i corresponds to that row. dp[i][0] will correspond to the min possible time taken to switch all the light off from row i to the last row having lights on if we start from left stairs and dp[i][1] will correspond to min time if we start from right stairs. dp[n][0] will be our answer. Substructure would be dp[i][0] = min(time taken to switch off all light on floor i + return back to left stairs + 1 +dp[i+1][0], time required to reach at right stairs + 1 + dp[i+1][1]) analogously calculate dp[i][1]. 1<=i<=N
I wrote above: http://codeforces.com/blog/entry/52318?#comment-363985
In problem D, isn't the graph a disjoint collection of DAG instead of forest of trees. So if it's a DAG then euler tour shouldn't work for correct solution! I mean there could be possible multiple root nodes for any node and so multiple ways to reach that node?
The graph is a collection of trees not DAGs since each child has at most one outgoing edge (to the child he depends on).
I have updated the tutorial statement. Please read it again and tell me if it is not clear.
For problem D, I think the ans for the case
3 2 4 1 1 1 2 2 3 2 3 1 1 2
is 2? (Child 1 and child 3 cry.) But I ran the implementation code, got answer 0.
This case is not valid. Child 3 can't request toy 1 while waiting for toy 2
Oh, thank you. I get it. I find the sentence "Some children are playing while others are waiting for a toy, but no child is crying, and no one has yet finished playing." in the problem description. So Child 2 hasn't finished playing now, then child 3 can't request toy 1.
Why did you color the leaf nodes as blue. What if I colored the leaf nodes with red and took the xor of the blue nodes.
I am new with game theory. Just trying to understand this variation of nim.
This is because you could only take away stuff at the leaf nodes, effectively that means nim is only played at nodes with even distance from the leaf.
I suppose it will be wrong because actions with leafs can't increase number of apples in any other vertex, so they must be treated like nim piles.
True!
Nim game with increases has two moves:
remove positive number of stones from one of the piles.
add positive number of stones to one of the piles.
We agreed that this problem has a solution similar to standard nim as proved in the link. The model I described in the editorial is equivalent to this variant: red -> blue is the second move and blue -> red/eat is the first move.
If took the xor of red nodes instead of blue ones, will this new model still equivalent to nim game with increases? The answer is no, because the move blue -> eat has no equivalent move in the variant (as if you are saying "take non-empty set of apples from nowhere and remove them away").
Why does the solution for D print 0 for this input:
Shouldn't 2 and 3 cry now?
This case is not valid because child 3 can't request toy 1 while waiting for toy 2.
Wouldn't child 3 wait for toy 2 and toy 2 would be released by child 1 after finite time? And only after that child 3 would request toy 1!
"No child keeps the toys forever." Why, if not for this reason, was this even mentioned in the statement??
But at the time scenario requests are made "No child has yet finished playing".
I see, thanks
Problem D was a bit puzzling by its rules. And you want to write something like
To decide that you should make oriented graph and find DSU in it and make something magic later to find if edge x->y can combine different DSUs...
Now I understand why this test is not correct, thanks.
In problem C you said "So, we can apply binary search", how do you come up with this conclusion from what already said before that? In other terms what are the conditions to apply bs.
If you have a monotonically increasing function f(x) and you want to find largest x such that f(x) ≤ k for some given k, then you can use binary search. Let our domain be limited to the range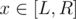 . We will try the midpoint m = (L + R) / 2:
. We will try the midpoint m = (L + R) / 2:
We go on search till we find the largest value.
For functions with YES/NO answers, the function must look like:
... YES YES YES NO NO NO NO ...
... NO NO NO YES YES YES ...
So, when you test a certain value, you will get information about the values before it or the values after it, so you can decrease your search space.
There is a nice editorial about binary search in this link.
Thanks.
@Ahmad_Elsagheer can we use binary search to solve knapsack problem. "what is maximum number of items we can peak if total capacity of knapsack is S"
The above solution solves it with binary search. DP is not possible because the state parameter for the remaining capacity can have n·107 different values which will not fit in time or memory.
My DP for problem B. submission
In problem C: Ques didn't mentioned that
Shageer must buy items consecutively. This ruined the problem.