Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
| Name |
|---|



We can solve problem E in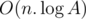 using two pointers: find the smallest range where product of numbers inside this range is divisible by k, then res = res + (n - end) * (start - previousStart) 28156236
using two pointers: find the smallest range where product of numbers inside this range is divisible by k, then res = res + (n - end) * (start - previousStart) 28156236
It's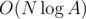 actually. For example test n = 1e5, k = 1 << 29, and a[i] = 2. You will iterate over each subrange of length 29.
actually. For example test n = 1e5, k = 1 << 29, and a[i] = 2. You will iterate over each subrange of length 29.
Oh, that's right. Thanks :)
for problem G we can build a flow network with only O(n) edges, so normal minimum cost max flow would work:
So we'll have 4 vertices for each array position, 2 of them are connected by an edge with cost -1, if this edge is part of the answer, then we would use this array position for one of the sequences, but we'll need to have a path from ai to every aj such that i < j and abs(ai — aj) = 1 or abs(ai — aj) % 7 == 0, for every array position i have an additional vertex which has a path to all those j > i such that ai = aj, we only need to connect this vertex to the first j which has the attributes mentioned, so we would only need to connect ai to the first j's additional vertex that is ai — 1, and the first j's additional vertex that is ai + 1 to have path to all such j's that aj = ai — 1 or aj = ai + 1, a similiar thing can be done for the modulo 7 part, with another additional vertex for every vertex (it can also be reduced to 7 overall, because there are only 7 modulos), you can see my code for better understanding
We can even simplify it to 3 vertices for each array position, so we'll have 3 * N vertices and 9 * N edges (in a worst case). Also, we can use dynamic programming approach to find initial potentials(like described in the editorial). So total complexity will be O(f*n*log(n)), where f = 4 => we have O(n*log(n)) solution,
Link to submission: http://codeforces.com/contest/818/submission/28193043
In problem G, am I mistaken by saying that almost everybody who solved it used a compressed graph with O(N) edges? That's what I understood from most of the sources: that for each i they add just about 3 edges backwards to the last j with +-1 different value or the same residuum modulo 7. Is that a correct approach? I haven't thought of some counter example but I cannot prove the correctness of this approach either...So could someone shade some light on this issue?
PS: Ok, it seems Reyna said about the same thing while I was typing the comment, so nevermind
For E, I built a sparse table of products of segments modulo k. It seemed simpler than fiddling with vectors of prime powers.
In E i used two pointers and queue, which can return (product of numbers inside) % k, similar to queue for finding min/max. Solution O(n) 28158111
Can you elaborate this technique ?
Here you can see the basics, it's easy to change for the product
I solved E with factorisation and then binary search (fix right border, binary search for left border). I am getting Runtime error on case 16 when n = 100000 and k = 1000000000. I tried some smaller n and k = 1000000000 and it works oK. Any ideas ?
http://codeforces.com/contest/818/submission/28159818
there's extra 0 here
if( k < 1000010 && is[k] == true ) kd.pb( k );
Unfortunatelly, that didnt fix :( Still, thank you for trying to help.
http://codeforces.com/contest/818/submission/28161706
If I'm not mistaken, my solution to F is O(1) : Solution I guess it's technically O(Q).
Math.sqrtworks in O(1) in java?Yup :)
It is same as the editorial, u just did the job of ternary search by hand.
I realize that, but when I actually implemented the ternary search, I got TLE so I resorted to this.
For Problem C,I have something puzzled.There is one sentence in problem,"Sofa A is standing to the top of sofa B if there exist two such cells a and b that ya < yb".Why ya < yb ?Should it be ya > yb?
Authors assume that y axis runs from top to bottom.
Agree, it is quite hard to imagine examples in this way.
In Problem C Editorial , shouldn't we decrement the result by 1 when x1i!=x2i instead of when x1i=x2i
Yes, I think it should be either x1i ≠ x2i or y1i = y2i.
Yup, you are right. Fixed, it will take some time to update.
For problem D, if cntA(n) = cntB(n) = 0 then which case should it be classified as? From the problem statement it appears that both Alice and Bob would win, but that sounds like a draw to me.
I dont think its a valid case as n >= 1 so either one of them will be greater than 0
Alice would not win. Alice's condition includes strictly greater sign, while Bob's has greater or equal.
8shubham, it is valid case though.
In Problem E I built a segment tree for modulo K so I can check if a segment [L..R] is divisble by K
It looked much easier that factorizing numbers and such
My Code
I did the same bro!! that approach is much easier..
Could somebody take a look into my solution for E? I can't understand why I got WA :( (Counting prime divisors in k first, then moving R until we have not enough divisors from k in current segment). Thanks in advance.
http://codeforces.com/contest/818/submission/28168045
EDIT: Oops, my fault.. I took sqrt(10^9) = 10^3 somehow..
Why do we have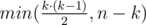 edges in connected component? Isn't it just
edges in connected component? Isn't it just 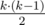 ?
?
Because we have to make the graph satisfy the property that at least half of the edges are bridges. Though we can connect at most k(k-1)/2 edges, we can add at most n-k edges (because we only have n-k bridges)
I see, thank you.
So,can I ask for the hack to problem A?
and fill the unvisited children with remaining values to form the permutation.
It doesn't make a difference in which order we place them?
Nope. We don't care about the order as we will never take these values.
For problem F why is building the graph as suggested optimal? How to prove it?
"Firstly you need to learn to factorize any number in no more than O(logn)." How can this be done ?
In general case you can run sieve of Eratosthenes in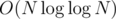 to calculate the smallest prime divisor of each number up to N. Then factorization will take
to calculate the smallest prime divisor of each number up to N. Then factorization will take 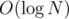 .
.
Here N is up to 109, so we decided not to take all the primes which is present in number but only those that are also present in k. And this is described in editorial.
So we do need a pre-computation using Sieve then. That is what confused me initially since that was not stated.
We don't. If the numbers were up to 105, for example, we could use it and don't even bother with all the useful primes. Please, reread the editorial. I believe, that everything needed is already stated.
Yeah I got it. Thanks !
I have a question for Problem F: since k * (k-1) / 2 is increasing and n-k is decreasing, wouldn't the maximal value of the function be at the index where k * (k-1) / 2 becomes greater than n-k? If that is true, could we just binary search to find the point where k * (k-1) / 2 > n-k, and get our answer from there? Submission: 28155258 (Sorry not so familiar with ternary search so just asking)
Yes that's correct.
f(k) is increasing when k ≤ k0 (asserted in the tutorial), because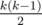 grows faster than (or as fast as, right at the peak) n - k decreases. Therefore k0 is the peak and can be found with binary search.
grows faster than (or as fast as, right at the peak) n - k decreases. Therefore k0 is the peak and can be found with binary search.
There is another (shorter and simpler than other solutions I saw) solution for E (it looks like
O(Nlog(MAXN)), but without binary search or something like this):We can start iterating through the array and stop when the product of prefix mod k is 0. Fix last index as
curEnd.If we have
curEnd == n-1and mod is not 0, stop iterating and print answer, because there are no more subarrays that are divisible by k.Then go left from
curEnduntil the product of elements mod k is 0.Now we have
lenof subarray that is divisible by k.We can add value
(curEnd - len + 2 - start) * (n - curEnd)to theanswer.In other words, we add all possible subarrays that contain our subarray (that is, array
[curEnd-len+1, curEnd]).Then update
start(it's 0 at the start of algorithm) tocurEnd - len + 2(startis the first index of subarray that we're gonna check on the next iteration, next value ofstartwill be the second element of just found 'good' array, so we won't count it twice or more).Then repeat the same algorithm, but starting with the new
start.So, why this solution is
O(Nlog(MAXN))?The worst case is when
k = 1<<29and the array consists only of 2's (i.e.[2,2,2,2,2...,2]).In this case
startwill be 0 at the first iteration, 1 at the second iteration and so on, but on every iteration there will belen=29(this islog(MAXN=1e9)).Link: 28180910
Does anyone know the proof for why in problem F the optimal solution will be achieved by having one large component and simply connecting the remaining vertices with bridges to it? If it's rudimentary, then let me know please so that I can think about it for some more.
Problem D statement is so difficult to understand
For 818F - Level Generation, there can be an O(1) solution.
Here is
a mathematical solution that does not require the ternary search. It only uses two values of k.Let, x be the variable k from the tutorial.
x = sqrt(2*n-1);n_minus_x = n - x;ans = min(x*(x-1)/2, n_minus_x) + n_minus_x;Another try
x = sqrt(2*n-1) + 1;n_minus_x = n - x;ans2 = min(x*(x-1)/2, n_minus_x) + n_minus_x;ans = max(ans, ans2);Note:
Code: 89187360
Hope it helps someone.
Edit:
Derivation of the formula:
x*(x-1)/2 <= (n-x)
-> x <= sqrt(2n-1)