Secret.Codes's blog

Odd even conditional function on Matrix exponentiation.
By Secret.Codes, history, 7 years ago, In English

Sometimes there are two different recursive function for even and odd n. Such as if n is even, then f(n) = f(n-1)/2, otherwise (if n is odd) f(n) = 3f(n-1) + 1.

I know basic of matrix exponentiation on many variation but now i am facing problem on it.

please someone explain.

  • Vote: I like it
  • +16
  • Vote: I do not like it

Comments Comments (9)
| Write comment?
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Not sure if there is a general way to handle such recurrences but for the current case, this should help: https://en.wikipedia.org/wiki/Collatz_conjecture

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can make both transitions at the same time. Consider n even, using your example we have f(n) = f( 3*f(n-2)+1 )/2. As n will always be even just need to apply this n/2 times. If n is odd just do one transition by hand and use the same method.

So use a new function, change the exponent properly and handle some corner cases.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +14 Vote: I do not like it

hx0 has written a Python decorator (description in Russian and English) which does exactly that. You can either read his description or my example here (or, actually, both):

General way:

First, write a program which solves the problem under the following limitations:

  • You're not allowed to use functions.
  • You're allowed to use a fixed number of variables only. No arrays, no dynamic memory.
  • You're allowed to use a single loop only, which goes for a specific number of iterations, which can be easily calculated from n.
  • You're only allowed to add variables together and multiply them by constants. You are not even allowed to add constants (although you're free to add an extra variable to hold value "one").

For example, here is the one for Fibonacci numbers:

prev2 = 0
prev1 = 0
for _ in range(n):
  prev2, prev1 = prev1, prev2 + prev1

And here is another for sum of squares (12 + 22 + 32 = 1 + 4 + 9 = 14). I'll go with this example from now on:

i = 1  # Current number
i2 = 1  # Its square, as we are prohibited from writing i*i
sum2 = 0  # Sum of squares of numbers [1..i)
one = 1  # Constant
for _ in range(n):
  sum2 += i2
  i2 += 2 * i + one  # (i+1)^2 = i^2 + 2 * i + 1
  i = i + one

Now, wonderful fact: the transformation you perform to that fixed set of variables on each iteration is actually a linear transformation which can be represented using matrix. You can see it that way: value of each variable after the iteration is some linear combination of values of variables before the iteration. In order to add constants, let's introduce For example, in the latter example we have the following transformation going on during a single iteration:

i_new = i_old + 1               = 1 * i_old + 0 * i2_old + 0 * sum2_old + 1 * one_old
i2_new = i2_old + 2 * i_old + 1 = 2 * i_old + 1 * i2_old + 0 * sum2_old + 1 * one_old
sum2_new = sum2_old + i2_old    = 0 * i_old + 1 * i2_old + 1 * sum2_old + 0 * one_old
one_new = one_old               = 0 * i_old + 0 * i2_old + 0 * sum2_old + 1 * one_old

Note that order of equivalences is the same as order of variables in each row — it's important, because now we're going to rewrite that transformation as a matrix:

 i i2  sum2 one
(1  1   0   1) * /1 2 0 0\ = (2 4 1 1)
                 |0 1 1 0|
                 |0 0 1 0|
                 \1 1 0 1/
(2  4   1   1) * /1 2 0 0\ = (3 9 5 1)
                 |0 1 1 0|
                 |0 0 1 0|
                 \1 1 0 1/
(3  9   5   1) * /1 2 0 0\ = (4 16 14 1)
                 |0 1 1 0|
                 |0 0 1 0|
                 \1 1 0 1/

Or, shortly:

 i i2  sum2 1
(1  1   0   1) * cubed /1 2 0 0\ = (4 16 14 1)
                       |0 1 1 0|
                       |0 0 1 0|
                       \1 1 0 1/

So, we've just transformed a simple loop iteration into a matrix. So, loop became matrix exponentiation and we can apply fast exponentiation trick.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +6 Vote: I do not like it

    UPD: I forgot to actually answer the original question. If you have different equations for odd and even values of n, you can pretend that you have two mutally recursive functions, e.g. instead of:

    f(2k) = f(2k-1) / 2
f(2k+1) = 3 * f((2*k+1)-1) + 1

    We would have:

    h(k) = f(2k) = f(2k - 1) / 2 = f(2*(k-1) + 1) / 2 = g(k - 1) / 2
g(k) = f(2k + 1) = 3 * f(2*k) + 1 = 3 * h(k) + 1

    And one can calculate these two recurrences simultaneously using the algorithm from above.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can two equation be relate all the time ?? I wanted a general solution .

      Is there any general solution???

      If the question is like f(n)=2*f(n-1)+6*f(n-5) if odd. f(n)=f(n-4)+f(n-5) if even. See now i have to think a lot to relate this two equation. So I want a general solution. If there is no general solution then is it possible to relate two equation all the time ?? If sometimes it is not possible then what should be done that time ??

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        General solution: if your formulas change every K steps, then you have to do K steps at once. If you have N functions which look at M steps behind to calculate, you'd have to use something like N × (M + K) variables to write the program I mentioned in my first post: just store last M + K values of each function and then calculate next K steps instead of only one step.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

http://fusharblog.com/solving-linear-recurrence-for-programming-contest-part-2/

→ Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I have a few doubts:
1. Does anyone know any question that uses the odd-even recurrence trick, as mentioned in the blog?
2. Is the Running time same as O(k3lg(n))?
3. Also is it possible to generalise this idea for solving a piecewise defined recurrence?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In my proposed general algorithm running time is still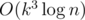 , if we say that k is the size of the matrix and n is number of iterations.

    What do you mean by "piecewise defined recurrence"? Can you give an example?

    → Reply