I recently saw at one blog , A code is executed like that
N + N/2 + N/3 + N/4 + ....... + N/N
and author of this code saying
N + N/2 + N/3 + N/4 + ....... + N/N = O(N log(N) ) ? How ?
We know complexity of something is divided by 2 , become log2(N) . For example binary search's worst case complexity is O(log2(N) ) . But how the upper snippet
N + N/2 + N/3 + N/4 + ....... + N/N
equals to O(N log2(N) ) ? Can anyone explain it ?










https://en.wikipedia.org/wiki/Harmonic_series_(mathematics)
Here it is: https://stackoverflow.com/questions/25905118/finding-big-o-of-the-harmonic-series
I can prove it that the complexity is less than or equal to O(n log2 n).
n / 1 + n / 2 + n / 3 + n / 4 + n / 5 + n / 6 + n / 7 + n / 8 + ... + n / n
is less than
n / 1 + n / 2 + n / 2 + n / 4 + n / 4 + n / 4 + n / 4 + n / 8 + ... + n / (2floor(log2n))
= n + n + n + n + ...
= n log2 n.
So the complexity is less than or equal to O(n log2 n).
thank you very much
In your (E869120's) way you can prove that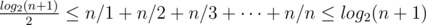 . Though, I think the base of logarithm is no need for representing time complexity. Because, comparing log2n and logen, you can see that log2n = logen × 1.44269..., for any positive n. 1.44269... is a constant, so it doesn't effect to time complexity. So I think the time complexity is O(nlogn), right?
. Though, I think the base of logarithm is no need for representing time complexity. Because, comparing log2n and logen, you can see that log2n = logen × 1.44269..., for any positive n. 1.44269... is a constant, so it doesn't effect to time complexity. So I think the time complexity is O(nlogn), right?