Hello Codeforces community! I decided to write tutorial about recurrent sequences, tutorial is about very basics of that topic. If you have little combinatorics knowledge, you will understand this tutorial easily. This is my first tutorial, so this can be easy for you and there can be mistakes. Probably all Div1 users knows all things in this tutorial :) Hope this tutorial will help you. If you have any questions/suggestions please write in comments.
Recurrent Sequences — Application of combinatorics in DP
Let’s start with a problem to this topic.
Problem. In how many different ways you can write 8 (+) and 5 (-) signs consecutively such that no two (-) signs are adjacent are adjacent.
Solution of problem is easy. Let’s write (+) signs after 9 ms:
m + m + m + m + m + m + m + m + m
Now let's change 5 of ms to (-) sign. Actually, problem has been solved, no 2 (-) signs are consecutive. So, answer is  (because there are 9
(because there are 9 ms and we have to choose 5 of them). Generally, if we have k (+) signs and r (-) signs, we can make 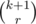 sequences such that no two (-) signs are consecutive.
sequences such that no two (-) signs are consecutive.
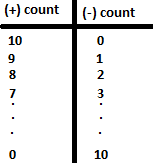
Problem. There are 10 signs are written on the board consecutively. How many different sequences we can create if some of them are (+) and some of them are (-) signs such that no two (-) signs are adjacent.
Let's think all situations:
With formula we found in previous problem answer is:
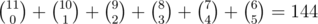
Generalized version of problem: If we have x signs which some of them are (+) and some of them are (-) signs, how many sequences we can create such that no two (-) signs are adjacent.
So, answer for this problem is
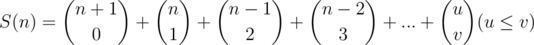
Let's write some few terms of S(n):
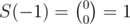 ,
, 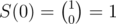 ,
, 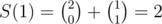 ,
, 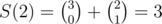 , S(3) = 5, S(4) = 8, S(5) = 13 etc.
, S(3) = 5, S(4) = 8, S(5) = 13 etc.
It remembered you something? Yes, Fibonacci numbers! Let's prove they are really Fibonacci numbers:
There are some proofs with Binet's formula, but we will prove this by strong induction:
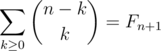
We verified some first terms. Assume it is true for - 1, 0, 1, .., n and we want to show that it is true for n + 1:
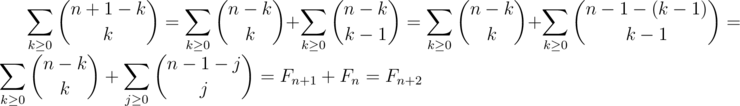
Problem. In how many different ways rabbit can go 10th step if it can jump 1 or 2 steps?
Well, we can solve this problem by analyzing some cases, but it will be hard way for calculating answer. So, let's think a little different. We can go 10th step from 9th step or 8th step, then answer for going 10th step is sum of answers for 9th step and 8th step. If F(n) is answer for going n'th step, we can calculate it by this recursive formula: F(n) = F(n - 1) + F(n - 2) with base cases F(1) = 1 and F(2) = 2.
Problem. (Hanoi towers) As you can see below there are 8 discs and 3 sticks. We can change places of discs with some rules: Only one disk can be moved at a time. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack. No disk may be placed on top of a smaller disk. Find minimum moves to move all discs to 3rd (left) stick.
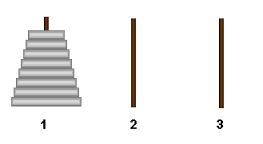
For solving this problem, let's think little cases firstly. If we had 1 discs, we could solve problem in 1 step. If we had 2 discs, first we put little disc to middle stick, then big disc to left stick, then little disc to left stick, so in 3 moves we could do it. There is a gif for doing this for 3 discs:

So, if we have n discs, we can solve problem like this:
Move (n-1) smaller than biggest discs to middle stick (*)
Move biggest disc to 3rd (left) stick (**)
Move (n-1) smaller than biggest discs to 3rd (left) stick (***)
We can't move biggest disc without taking other. If 3rd (left) stick is not empty, we can't put biggest on it. So, using this 2 facts it is the best strategy to solve problem. Let H(n) be answer for n discs. Then we can do (*) and (***) in H(n - 1) steps and (**) in 1 step. So, we can calculate H(n) by this recursive formula: 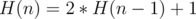 .
.
So, we can solve this problem in O(n) easily. But, what about if n is very big, like n ≤ 1018, for this constraint we have to make faster algorithm. Let's write first few terms of H(n):
H(1) = 1, H(2) = 2 * H(1) + 1 = 3, H(3) = 2 * H(2) + 1 = 7, H(4) = 2 * H(3) + 1 = 15 etc.
It is not hard so see H(n) = 2n - 1, so let's prove it by induction:
We show it is correct for first few terms
Assume that H(n - 1) = 2n - 1 - 1 and show H(n) = 2n - 1
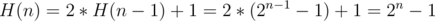
Prove is done!
Problem. There is a park station such just Cadillac, Continental and Porsche (yeah, very expensive station) can park there. Cadillac and Continental are big cars, so they need 2 "car place" to park and Porsche needs 1 "car place" to park. If there are n "car places" in park station find out in how many different ways cars can park at station. (It is not important to park all types of cars).
Let P(n) be answer for n "car places". If Porsche parks at first "car place", answer for remaining (n-1) places is P(n - 1). If Cadillac parks at first two "car places", answer for remaining (n-2) places is P(n - 2) , same thing for Continental. So our recurrence relation is:
P(n) = P(n - 1) + 2 * P(n - 2) and bases cases are P(1) = 1 and P(2) = 3 (easy to show).
Challenge Problem. Write code which solves previous problem for n ≤ 1018 constraint.
Challenge Problem. n runners will do a race. Some runners can pass finish line at the same time, for example, 6th runner finished race 1st, 2nd and 5th runners finished race 2nd and other 3rd. How many different results of race can be there?
P.S. Finally, I finished this tutorial :) Writing tutorial is really hard. I'm really sorry for some mistakes, please write if you have question.











Seems I have haters :\ Got -5 in 1 minute
Very grateful for the first and last tasks :)
Good work TooNewbie !
good work .
Thank you for the tutorial! I think there is another interesting combinatorial proof for the first problem.
Let an be the number of sequences of length n comprised of "-" or "+" signs such that no two "-" signs are adjacent. Let bn be the number of such sequences that end with "-", and cn be the number of such sequences that end with "+".
Then we get the recurrences bn = cn - 1, cn = cn - 1 + bn - 1 = cn - 1 + cn - 2, since we can only generate a string that ends with "-" by appending a "-" to a string that ends with "+", but we can get a string that ends with "+" by appending "+" to any string.
Now since c1 = 1, c2 = 2, it is evident that cn follows the Fibonacci recurrence, and so does bn (except it's shifted one index back). Then it follows that an = bn + cn = cn - 1 + cn = cn + 1 = cn + 2, and so an follows the Fibonacci recurrence as desired.
This proof is similar with solution of Parking Places problem :)
Is there any direct formula for first challenge problem? I have tried my best but only succeeded in reducing the number steps by some factor. If there is any direct formula can you please explain it?
Well, the easiest way is matrix exponentiation, but there is better way:
We will write characteristic equation, let c be constant then our equation is:
cn = cn - 1 + 2cn - 2
c2 = c + 2 and c2 - c - 2 = 0
We get c = 2 and c = - 1. So, for some x, y,
P(n) = x * 2n + y * ( - 1)n
Also, we know that P(1) = 1 and P(2) = 3, lets write this terms with x, y:
P(1) = 1 = 2x - y
P(2) = 3 = 4x + y
From this system, we get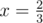 and
and 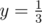
So, final answer is:
Great method! Thank you :D This method only works when there are real roots of the characteristic equation. Isn't it?
Well, I didn't faced with problem which doesn't have real roots of its characteristic equation, but it would be weird, because if it hasn't real roots then it means this function is decreasing function, and with big values you will get big negative numbers, and if they ask you to find it MOD M, you can (not in some cases) modify problem for solving it with characteristic equation.
And it is very standard matrix exponentiation problem, there are not very good resources for learning it, but this + practice problems will do work.
Thank you for your reply. I'll try out this method with other recurrences to understand it in a better way. For matrix exponentiation I found this blog which helped me in understanding it.
If you want to calculate some weird function like a*(x+sqrt(y))^n+b*(z+sqrt(y))^n mod p you can do it using fast exponentiation and storing a number like a+b*sqrt(y) mod p.
Let memo[x] be the answer for x runners. memo[0] = memo[1] = 1.
If there are n people in a race, we can tie anywhere from 1 person n people for the top spot, and recurse with (n-(numberOfTiedPeople)) people to calculate the number of ways to fill in the rest of the spots.
We can calculate memo[n] as follows:
for(int i = 1; i <= n; i++) memo[n] += memo[n-i]*choose(n, i);Credits to matnakash and CF Discord
Yes, that is correct solution :))
Why downvoted?
May you clearify more please !
is a Bell number wikipedia
challenge problem 1 can be visualised as follows: multiply matrix|1 2||1 0|(2x2) as many times as n and p(n) is the first element of that
resulting matrix, and that multiplication can be done in O(log(n)) ....
Excuse me sir :),it's "Hanoi tower",not "Hanio tower".Can you correct it please?
Ah, sorry. Corrected :)
Does second challenge problem has any O(n) solution ? I could only figure out O(n^2) trivial algorithm.