The Nordic Collegiate Programming Contest (NCPC) 2017 will be held tomorrow. It is the subregional ICPC contest for Denmark, Finland, Iceland, Norway, and Sweden.
There will also be an open contest in which anyone can participate. The open contest will begin at the same time as the official contest, Saturday October 7 UTC 9:00, and its duration is five hours.
Welcome! You can also discuss the problems here after the contest.











How to solve problem D ?
Graph of masks and bfs from each mask from input. Graph contains the edge if two masks are different only on one bit. The answer is a vertex with the biggest distance.
We solve 7 problems and didn't solve this problem , omg..!!!
Ty!
What is the name of your team?
LeXaHam
How to solve C?
zscoder your team is "Soromonogatari" ?
Yes
Do you solve problem F?))
Yes (actually my 8th submission is already AC and I submitted the cleaned version after that because I thought it won't count though apparently the scoreboard says 0+9 instead of 0+8)
Can you explain solution ?
Let f(u, v, k) denote the distance of node u and v in Fk. From now on, we assume u ≤ v for convenience.
Let L denote the number of leaves of F0.
If L = 1, the answer is just v - u since the tree is a path. Thus, we assume L > 1.
Note that the size of Fk is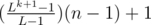 .
.
Note that the tree Fk can be constructed by replacing each leaf of F0 with a copy of Fk - 1. (note that this is slightly different from the original defintion but you can prove that they're equivalent)
Thus, each node in the original tree corresponds to a range of nodes in Fk. Specifically, each non-leaf node in the original tree will correspond to one node in the final tree and each leaf node will correspond to S(Fk - 1) nodes in the final tree, where S(Fk - 1) is the size of Fk - 1, which can be computed with the formula above.
The main idea to calculate f(u, v, k) is to first check which node in F0 contains u and v then try to recurse downwards.
Now, if k = 0 we can compute the answer directly from the original tree (note that you need to precompute heights and LCA to answer this in ).
).
Let's first consider the naive solution.
Iterate through the nodes of F0 one by one in depth-first manner to determine which node u and v corresponds to. Let u' and v' be these nodes. Then, there are a few cases :
If u and v corresponds to non-leaf nodes, return dist(u, v) and we're done.
If u corresponds to a leaf node and v doesn't, then return dist(u', v') + f(0, u - S, k - 1), where S denotes the number of nodes in Fk encountered before we reach the node containing u. Similarly, we can do a similar recursion if v corresponds to a leaf and u doesn't.
If u and v both corresponds to leaf node, then if u' = v', return f(u - Su, v - Sv, k - 1) (Su is number of nodes in Fk encountered before reaching u and Sv is similar) and if u' ≠ v', return dist(u', v') + f(0, u - Su, k - 1) + f(0, v - Sv, k - 1).
This solution should work in O(kn) time (we omit the time required to calculate size of Fk for simplicity), which is clearly too slow.
The first optimization that can be made is to speed up the process of finding u', v' and Su, Sv. Let's do a dfs on the tree and for each node u, store a pair (x, c), where x is the number of nodes encountered till now and c is the number of leaves encountered till now. Then, the total number of nodes in Fk encountered up to u is x + c·(S(Fk - 1) - 1).
With this, we can do a binary search and determine which nodes u and v correspond to in F0 in time. However, the complexity is still
time. However, the complexity is still 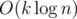 , which is unacceptable.
, which is unacceptable.
The next optimization is to note that if k is large, for example when k > 32, the value of S(Fk) will definitely exceed 230. Thus, a lot of calculations can be omitted. Indeed, when we reach the case where u' = v', and let S denote the number of nodes in F0 encountered before u', then we'll keep calling the functions f(u, v, k), f(u - S, v - S, k - 1), f(u - 2S, v - 2S, k - 2), ... until k ≤ 32 or one of the arguments become less than S. We can calculate exactly when this happen with some math and from there we can switch to the case f(0, v, k).
For f(0, v, k), the process is similar, except the answer will be increased by H, the height of v' in F0 each time you recurse down, so you need to add a multiple of height of v' to the answer.
Thus, each query can be answered in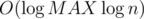 time, and the total complexity is
time, and the total complexity is 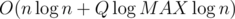 .
.
Thank you!!
Keep track of the cards' uniqueness for each colour individually.
For any one colour, first sort the cards by their angles and then put them in a linked list. You can quickly work out the card's score contribution for this colour as either
uq(x) = dist(x.prev,x) + dist(x,x.next), or just 0 if it has a neighbour with the same angle.Every time you remove a card, the only scores that might change are the scores of its neighbours in the linked list, so recalculate both of them every time you delete something.
To get the overall least-unique card, keep a global set<pair<Value, ID>> and make sure to update it every time you change the score for a particular colour. You can repeatedly pop the smallest element off that set, update the small number of affected nodes, and repeat until there's nothing left.
Right, for some reason I somehow thought this wouldn't work but now I feel dumb. :P Thanks.
I use the
priority_queueinstead ofset, because I worry thatset.find()can't find the exact element.when will the scoreboard be unfreeze?
anybody knows how to fix WA 12 (Problem H)?
Our solution: for each citizen find left & right train by sorting citizens & trains as events by polar angle, then for each citizen we are determine closest train (if it only one, we connect them immediately, otherwise we assign citizen to the sector between two trains). After that step only citizens between two trains left and we are find sector with smallest amount of citizens (it needs to achieve O(N) and fits to TL) and just try every possible assignment to the left train in this sector — at the other sectors we can make greedy assignment. I can't break this solution.
The idea of your solution is correct, so most likely you have a bug in the implementation. The test data used in the contest will be published.
Thanks, please let me know, when test data will be published
When and where will be the test data of contest will be published?
It is now available here.
Most likely you failed in determining "closest train". I used eps = 1e-9 and failed, while eps = 1e-13 plus long double gave AC.
Hmm, I thought about it, but I can't imagine test since coordinates only up to 1000 (I supposed that worst case for this is two rays (minX, maxY) and (maxX, minY) and test point (maxX, maxY — 1)).
I don't know the tests, but my line of thinking was :
After contest EndTime told me that 1e-12 gives WA, so probably there is a test about that
Thank you! I got AC with 1e-13 eps, very surprising!
How to solve problem K? I don't know how to check feasibility after binary searching over the answer.
The official solutions can be found here.
Thanks! But I still can't understand the way in the solution and I tried many times but always WA.
just do a greedy? basically for each kayak, find the smallest pair that fulfill the required speed?
Thank U!!! I got it