My solution depends on the following hypothesis. Can anyone prove this?
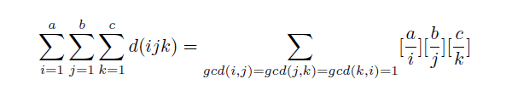
Sorry, the image doesn't work for some reason. \sum_{i=1}^{a} \sum_{j=1}^{b} \sum_{k=1}^{c} d(ijk) = \sum_{gcd(i,j)=gcd(j,k)=gcd(k,i)=1} [\frac{a}{i}][\frac{b}{j}][\frac{c}{k}] Now it works.
Sorry, please type "http://rng.gozaru.jp/cf.png" directly to the address bar.
Finally proved: "http://rng.gozaru.jp/b.pdf"










Image is not shown because of 403 error
I have thought about it for a long time...still can't understand it...It's like magic...
I think it can even be extended to 4 or larger number.
Sure. Proof will be the same
Does this couclusion can still be hold in more general form ? .. .
Can we prove it by Möbius_inversion_formula ? .
Your proof one could easily reformulate without telescopy. We have sum of d(ijk) -- number of triples x, y, z pairwise coprime divisors of i, j, k respectively. Consider how many times we count any triple of coprime integers x, y, z. Obviously it is a product of their multipliers numbers, it equals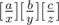
Thanks for the neat and instructive proof.