I've been thinking for one month and I still don't know how to solve this problem:
There is a park of size (A<=100)x(B<=100) (consider it as a grid), with (1, 1) as the top-left corner. There are C<=1000 trees on the park, all of which have distinct locations. You want to place as many VIP lounges on the park as possible, such that every VIP lounge is adjacent to a tree on its top, bottom, left, or right. But because of privacy issues, a VIP lounge cannot be adjacent to another VIP lounge (including diagonally). Note that you cannot place a VIP lounge on a tree.
For example, consider the following park of size 9x7:
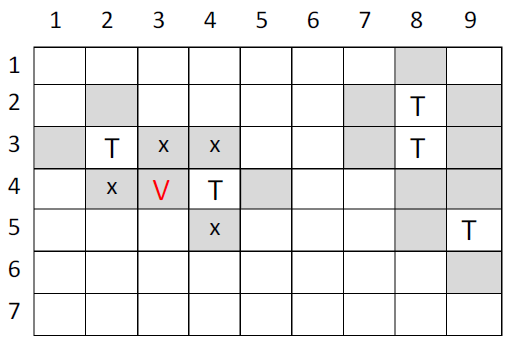
The "T"s represent the trees, the grey shaded areas represent possible locations for VIP lounges. If there were to be a VIP lounge on where the "V" is located, then the "x"s represent the locations where there cannot be VIP lounges.
Time limit: 1s
My thoughts:
Finding the maximum independent set of a bipartite graph can be done in polynomial time. Create a graph in which the possible VIP lounge placements are nodes and there are edges between 2 nodes if the 2 VIP lounges are adjacent. The maximum independent set of this graph is the answer. Notice that this graph is quadripartite (all combinations of x, y mod 2). Maybe there is also a way to find the maximum independent set of a quadripartite graph efficiently.
Or maybe I'm thinking too much and there is a greedy solution.










I'm also curious about the official solution of this problem. I ever thought on this problem for a full night and didn't get any idea. But you should know... sometimes, the quality of problems in Taiwan is terrible. It may be an open problem.
In fact, it is a planar graph. Unfortunately, maximum independent set on planar graph is still NPC.
First, showing the graph in a problem is planar and the fact that MIS on planar graph is NP-hard don't imply this problem is NP-hard. (As it may only encounters a certain kind of planar graphs, e.g. MIS on trees)
Second, it's NOT planar graph.
All "X" should be a node, and it's not planar. (you can find K_5 as a minor)
What is the time limit of this quesion? My team just practiced with the 2014 TaiChung problem set, and now my attitude is pretty much — "Does it has a 60s Time Limit? YEAH JUST GO AHEAD BRUTE FORCE TILL WE GET CHAMPION".
Or maybe it just have some really weak test cases — https://icpcarchive.ecs.baylor.edu/index.php?option=onlinejudge&page=show_problem&problem=5014
Thanks for mentioning it, the TL is 1s.
To clarify, the problem described in the post is actually from a programming contest for high school student in Taipei city in Taiwan not from ACM-ICPC Taiwan regional.
Though some problems from Taiwan regional actually has weak test cases, I'm not sure whether that is a correct example. Some problems uploaded to ACM-ICPC Live Archive has only included sample tests(or some random permutation of it). But, those problems indeed have stronger tests during the official contest. For example, some problems from the daejeon regional in 2016 contains only sample tests.
Auto comment: topic has been updated by tmwilliamlin168 (previous revision, new revision, compare).
tmw orz
tmw orz
tmw orz
How to solve this?
potentially useful, but there's a version of this problem where there's another constraint where the number of VIP lounges in each row/col is specified. This version is one puzzle of Simon Tatham's Portable Puzzle Collection with his approach described here