http://www.spoj.com/problems/BORING2/
The problem asks to compute 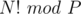 for prime P
for prime P
where

Unfortunately, 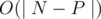 doesnt pass!
doesnt pass!
UPD: I have thought about an alternate approach by calculating factorials using their prime factorization (Legendre's formula). But I am not sure if it is fast enough.











Wilson's Theorem looks like a logical first step. The problem reduces to the main difficulty of finding N! mod P for N<= 1e6.
There are many speedups for computing N! mod p apparently (as I just found by Googling). I'm not sure which solution is intended, but it seems that https://en.wikipedia.org/wiki/Montgomery_modular_multiplication might come in useful for a "constant factor" speedup.
http://www.geeksforgeeks.org/compute-n-under-modulo-p/ also looks interesting.
Since you wrote O(|N-P|) you probably know this already, but it's faster to compute N! then take the inverse than multiplying inverses of 1 through N.