Hi, good day to U'll.
I have the following equation :
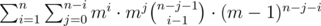 =
= 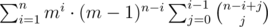
Can you help me with a proof for this ? BTW, this relates to the last part of the following problem : Link. The editorial for the problem tells us to convert the lhs to the rhs w/o any proof or explanation on how it is obtained. Any help would be useful
Thank You











Don't reuse i and j on both sides — it is misleading because the i/j on the left side don't correspond to the i/j on the right side (notice the editorial doesn't do this either).
W.r.t. rewriting, let's start with the left hand side. Notice that there is both an mi and an mj term that we can take together to mi + j. Additionally, notice that we can write (m - 1)n - j - i as (m - 1)n - (i + j). Now we have the term (i + j) twice — at this point you can fiddle a bit with the binomial coefficient and notice that C(n - j - 1, i - 1) = C(n - (i + j) + i - 1, i - 1). In other words, in addition to the (i + j) term, we also have a (i - 1) term appearing twice now.
At this point the correspondence should be clear if you look at both sides: the i on the right is the (i + j) we just factored out on the left, and the j on the right is the (i - 1) we just factored out. Now all you need to do is fix the summation bounds.
Got it, we iterate on the Binomial coefficients on the basis of their (i + j) values, (Bring all terms having same (i + j) together, and then try to get to the rhs).And maximum possible value of (i + j) is n.
So we can rewrite the left-hand side to:
The point is that in this expression, we see the terms (i + j) and (i - 1) repeat, and so we might consider looping over those instead of i and j. So we just define s = (i + j) and t = (i - 1). Then the terms we are summing can also be written as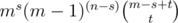 . They are still the same terms, it's just that I substituted s = (i + j) etc where possible.
. They are still the same terms, it's just that I substituted s = (i + j) etc where possible.
So then the only question is: how can I sum over s and t such that I end up with the exact same terms as when I summed over i and j?
We know that 1 ≤ i ≤ n and 0 ≤ j ≤ n - i. Rewriting the second gives us i ≤ i + j ≤ n, so from this we can conclude (since s = i + j) that 1 ≤ s ≤ n. Since we now also have 1 ≤ i ≤ s, we can also conclude (since t = i - 1) that 0 ≤ t ≤ s - 1. Those are your summation bounds.
I got it 100%, I'm thankful to you for your time. :)