Hello.
On December 17th at 07:00 UTC we are hosting the second elimination round of our olympiad for high school students. More information on olympiad's website.
Contest in gym: Innopolis Open, Elimination round 2, 2017-2018
We hosted the first round Innopolis Open, Elimination round 1, 2017-2018 on December 2nd. Those, who already advanced to the final round, can skip the round, but certainly can participate if they want.
The problems are prepared by dusja.ds, burakov28, julsa, KamilBek, josdas, budalnik, disa, lightning, VArtem, pashka, niyaznigmatul, FireZi, iilnar. We thank the developers of PCMS for testing system, we also thank ilsaf13, who does the technical support of our olympiad. We thank the testers of the rounds craborac, demon1999, haposiwe, zclimber, YakutovDmitriy.
We can discuss problems after the round here.
Good luck all!











Where can we find those who qualified from first round?
UPD: List of those qualified is here: https://olymp.innopolis.ru/ooui/innopolis-open-2017-2018/standings/all-final_en%20(1).html
Damn you were really close :)
zscoder, prepare your solutions beforehand, please.
For problem E, is there a deterministic approach? I used a probablistic one to try and find the best partition, but got only 50 points.
Yes, sure. The problem can be reduced to Knapsack-problem, and since the weights are small enough (linear on the input length), it can be solved in polynomial time. You still have to do several optimization (they are deterministic) to get full score.
Yes, I saw that with knapsack we can solve it in O(N2). What optimizations are you talking about?
Note that there are not many distinct weights. Also use bitsets to restore solution.
My solution works in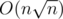 time (which might be a bit tight but it managed to pass on first try.) and
time (which might be a bit tight but it managed to pass on first try.) and 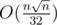 memory. Currently I'm not home so I don't have time to describe my entire solution but that should be my solution's complexity.
memory. Currently I'm not home so I don't have time to describe my entire solution but that should be my solution's complexity.
I see. The weights represent differences between pairs, and the sum of all values of all pairs is N, therefor there are at most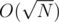 distinct values. So we can do knapsack in
distinct values. So we can do knapsack in 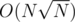 time, and in order to also maintain the actual sets we can use a bitset, which divides the memory by 32.
time, and in order to also maintain the actual sets we can use a bitset, which divides the memory by 32.
By the way, the best way to pick coefficients is by picking primes, the coefficient 1 and the pairs {1, 0}, {1, 1}? This is what I did and I think it's optimal but I'm not sure how to prove it. Edit: nevermind it's actually easy to prove.
Although there may be at most sqrt(n) different values, how do you update the dp with only O(1) each time for a value, even if that value has multiple occurrences?
Let dp[i][j] be the minimum number of type j numbers to get a sum of i assuming we use first j types. (-1 if impossible)
dp[i][j] = 0 if dp[i][j - 1] ≠ - 1.
dp[i][j] = dp[i][j - a[i]] + 1 if dp[i][j - a[i]] ≠ - 1 and dp[i][j - a[i]] + 1 ≤ cnt[j] (cnt[j] is the number of elements of type j we can use)
Note that you only need to store two rows of dp each time, so you can do this in O(N) memory. The state transitions are clearly O(1).
Also, to restore the answers, you can use a bitset for each type as "parent" array to backtrack and find solution.
Hi! How to solve a problem B for 100% ? I solved it only for 17% . Can you give a hint or an algorithm ?
You don't need to test every single value of i, there are only a few values of i that matter (I tested 10).
And how i can find a value of i ?
check a,b,c,d,1,n ± 1
Where can I find problems? Can I submit somewhere?
For the last elimination round, they created a gym with the problems from that round.
Here: Отборочный этап Олимпиады Университета Иннополис. Второй тур. 2017-2018
Full solution to C. Credits: niyaznigmatul, 300iq.
If n and m are odd, answer is -1.
If sum of array is negative, answer is -1.
Otherwise, we can always find an answer.
Take an arbibtrary cycle. For example, when m is even we can take:
Similarly, when n is even we can take:
Write down numbers in this order and compute prefix sums p1, p2, ..., pn * m. Let k be the index of minimal number among them.
Now, repeat this cycle infinitely many times and compute prefix sums on it again — p1, p2, ..., pn * m, pn * m + 1, ..., p2 * n * m, ....
You can notice that there is no pi < pk for any i > k. From this you can infer that pi - pk ≥ 0 for all i > k. This means that we can take a cyclic shift of this cycle and put k-th element in the end and this will be the correct answer (since there will not be such i that p'i < 0, where p' is a prefix sum array for this new cyclic shift).
Can somebody show me code of B?
Where the editorial?
deleted