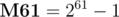
It is easy to calculate modulus using this prime (with bitwise operations, it is well known)!
My question is how can we efficiently calculate 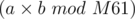 , where a and b can both have at most 61 bits.
, where a and b can both have at most 61 bits.
UPD: Found a function here that multiplies 64 bit with 32 bit while maintaining modulo. Can it be extended for 64 bit multiplied with 64 bit efficiently?











From http://codeforces.com/blog/entry/1729?locale=ru#comment-32989