Hello, Codeforces!
Some time ago I invented an interesting data structure and I'd like to share it with the community. Maybe, it was known before, and if you knew about it before my blog post, please share the link to the source.
What can the data structure do?
Given an array a that contains n elements and the operation op that satisfies associative property: (x op y)op z = x op(y op z) is true for every x, y and z.
So, such operations as gcd, min, max, sum, multiplication, and, or, xor, etc. satisfy these conditions.
Also we have some queries l, r. For each query, we need to find al op al + 1 op ... op ar. Let's call such queries q(l, r).
My data structure can process such queries in O(1) time with 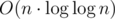 preprocessing time and
preprocessing time and 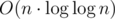 memory.
memory.
How it works?
1. Sqrt
Let's do a sqrt-decomposition. We divide our array in  blocks, each block has size
blocks, each block has size  . For each block, we compute:
. For each block, we compute:
- Answers to the queries that lie in the block and begin at the beginning of the block (prefix-op)
- Answers to the queries that lie in the block and end at the end of the block (suffix-op)
And we'll calculate another one thing:
between[i, j]i ≤ j -- answer to the query that begins at the start of block i and ends at the end of block j. Note that we have blocks, so the size of this array will be
blocks, so the size of this array will be 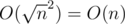 .
.
Let's see the example.
Let op be + (we calculate sum on the segment) and we have the following array a:
1 2 3 4 5 6 7 8 9
It will be divided onto three blocks: 1 2 3, 4 5 6 and 7 8 9.
For first block prefix-op is 1 3 6 and suffix-op is 6 5 3.
For second block prefix-op is 4 9 15 and suffix-op is 15 11 6.
For third block prefix-op is 7 15 24 and suffix-op is 24 17 9.
between array is:
6 21 45
- 15 39
- - 24
It's obvious to see that these arrays can be easily calculated in O(n) time and memory.
We already can answer some queries using these arrays. If the query doesn't fit into one block, we can divide it onto three parts: suffix of a block, then some segment of contiguous blocks and then prefix of some block. We can answer a query by dividing it into three parts and taking op of some value from suffix-op, then some value from between, then some value from prefix-op.
But if we have queries that entirely fit into one block, we cannot process them using these three arrays. So, we need to do something.
2. Tree
We cannot answer only the queries that entirely fit in one block. But what if we build the same structure as described above for each block? Yes, we can do it. And we do it recursively, until we reach the block size of 1 or 2. Answers for such blocks can be calculated easily in O(1).
So, we get a tree. Each node of the tree represents some segment of the array. Node that represents array segment with size k has 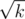 children -- for each block. Also each node contains the three arrays described above for the segment it contains. The root of the tree represents the entire array. Nodes with segment lengths 1 or 2 are leaves.
children -- for each block. Also each node contains the three arrays described above for the segment it contains. The root of the tree represents the entire array. Nodes with segment lengths 1 or 2 are leaves.
Also it's obvious that the radius of this tree is 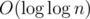 , because if some vertex of the tree represents an array with length k, then its children have length
, because if some vertex of the tree represents an array with length k, then its children have length 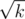 .
. 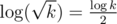 , so
, so 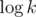 decreases two times every layer of the tree and so its height is
decreases two times every layer of the tree and so its height is 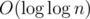 . The time for building and memory usage will be
. The time for building and memory usage will be 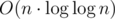 , because every element of the array appears exactly once on each layer of the tree.
, because every element of the array appears exactly once on each layer of the tree.
Now we can answer the queries in 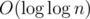 . We can go down on the tree until we meet a segment with length 1 or 2 (answer for it can be calculated in O(1) time) or meet the first segment in which our query doesn't fit entirely into one block. See the first section on how to answer the query in this case.
. We can go down on the tree until we meet a segment with length 1 or 2 (answer for it can be calculated in O(1) time) or meet the first segment in which our query doesn't fit entirely into one block. See the first section on how to answer the query in this case.
OK, now we can do 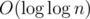 per query. Can it be done faster?
per query. Can it be done faster?
3. Optimizing the query complexity
One of the most obvious optimization is to binary search the tree node we need. Using binary search, we can reach the 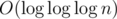 complexity per query. Can we do it even faster?
complexity per query. Can we do it even faster?
The answer is yes. Let's assume the following two things:
- Each block size is a power of two.
- All the blocks are equal on each layer.
To reach this, we can add some zero elements to our array so that its size becomes a power of two.
When we use this, some block sizes may become twice larger to be a power of two, but it still be 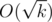 in size and we keep linear complexity for building the arrays in a segment.
in size and we keep linear complexity for building the arrays in a segment.
Now, we can easily check if the query fits entirely into a block with size 2k. Let's write the ranges of the query, l and r (we use 0-indexation) in binary form. For instance, let's assume k = 4, l = 39, r = 46. The binary representation of l and r is:
l = 39(10) = 100111(2)
r = 46(10) = 101110(2)
Remember that one layer contains segments of the equal size, and the block on one layer have also equal size (in our case, their size is 2k = 24 = 16. The blocks cover the array entirely, so the first block covers elements (0 - 15) (000000 - 001111 in binary), the second one covers elements (16 - 31) (010000 - 011111 in binary) and so on. We see that the indices of the positions covered by one block may differ only in k (in our case, 4) last bits. In our case l and r have equal bits except four lowest, so they lie in one block.
So, we need to check if nothing more that k smallest bits differ (or l xor r doesn't exceed 2k - 1).
Using this observation, we can find a layer that is suitable to answer the query quickly. How to do this:
For each i that doesn't exceed the array size, we find the highest bit that is equal to 1. To do this quickly, we use DP and a precalculated array.
Now, for each q(l, r) we find the highest bit of l xor r and, using this information, it's easy to choose the layer on which we can process the query easily. We can also use a precalculated array here.
For more details, see the code below.
So, using this, we can answer the queries in O(1) each. Hooray! :)
Conclusion
We have a data structure that asymptotically answers the queries on a segment very fast. But, the constant of this data structures is big enough. Also it doesn't support changing the elements. But it can be modified to perform modification queries in something about  for modifying a single element. But in this case, query complexity becomes
for modifying a single element. But in this case, query complexity becomes 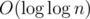 . You can think how to do this as an exercise.
. You can think how to do this as an exercise.
Problems
https://www.codechef.com/NOV17/problems/SEGPROD
Code
If you have some suggestions on how to improve this data structure or how to modify it, or something is written unclear and needs more explanation, feel free to write in the comments.
UPD: As it's noticed in the comment, this algorithm (and some more optimal ones) can be found in this article (thanks Rafbill).
UPD2: As geniucos described in the comment, we can improve the time complexity to 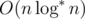 for preprocessing if x op x applies. Let the block size is
for preprocessing if x op x applies. Let the block size is  , not
, not  . We use a sparse table instead of between array. We will have
. We use a sparse table instead of between array. We will have 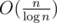 blocks and time complexity for building a sparse table will still be
blocks and time complexity for building a sparse table will still be 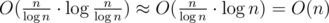 . The tree will have much smaller layers and we still have O(1) per query.
. The tree will have much smaller layers and we still have O(1) per query.
UPD3: The code is adjusted to work with non-commutative operations. The commutative property removed from the post.
UPD4: Continuation of the post











Auto comment: topic has been updated by gepardo (previous revision, new revision, compare).
Fix preprocessing complexity in the title :)
Thanks, done :)
I have been a regular participant and a coder at this amazing website for more than an year now. Lately some folks have been trying to malign its image by spamming shit and polluting the environment of this wonderful community. But thanks to people like you (gepardo), who are here to always share their knowledge with noobs like us. :)
Thank you (:
See https://pdfs.semanticscholar.org/cf74/0240d3a7440e23e92a09bf590cb70544cf4f.pdf. Your algorithm is be the same as their algorithm to answer queries in 3 steps.
Wow, that's interesting :) Thanks for finding this paper. I will update the blog post to mention it. So, the best algorithm for performing queries on a segment is O(α(n)) per query and O(n) per preprocessing?
So, Alternative for sparse table?
Pretty interesting! Also, the tree really reminded me of this one, by the concept of dividing the segments recursively to a size of sqrt the length.
Very nice!
I first came to know this idea when I studied the solution to IOI 2006 problem Pyramid
https://wiki.ioinformatics.org/w/images/f/f1/Ioi06pyramid_sol.pdf
There are many different (but related) ways to solve this typical "data-structure" problem, but the official solution is essentially your block or "single level tree". I never thought about "iterating" that same idea, probably because of how common and simple Segment Trees / Sparse Table are in competitive programming, but the achieved complexity is very nice indeed.
I imagine that for typical programming-contest array bounds, a direct implementation with a constant and fixed depth of 3 or 4 should work very very fast in practice.
Is commutative property actually required? I've just gone really quickly through the blog and it seems that only associative one is used. Am I wrong?
LE: I've just looked at the above-mentioned article and the method seems to work on any semigroup. Your implementation, however, seems to make use of the existence of a 0 (element e), so it works on monoids, although I'm pretty sure it can be slightly altered to work on semigroups as well
It does say "not required, optional" in the blog itself.
Shit, you're right. I haven't seen that. Sorry
Сommutative property is not required, but if your op has commutative property, you can think of less details (how to order the elements in the operation). But the code can be easily adjusted to take care of non-commutative operations, too.
Actually, my implementation works on semigroups, existence of zero-element is not required:
Elements which we use to make the array size 2k can be any, because they will not be used in query.
ansvariable to calculate between, is also not required to be zero in the beginning because of this line:ans = (i == j) ? add : op(ans, add);So, then i = j, it doesn't do
op(0, add)but simply assigns toadd.Yes, you're right indeed. Also I'd like to stress that your method can work in Nlog*(N) complexity if you have the following extra properties:
If you have those you can split the array in parts of logN instead of sqrtN and apply the same thinking. And it will work because you can overlap segments, given that applying x several times doesn't actually matter. This works for example for min, max, gcd, and, or
Interesting :)
To achieve such complexity, we build a sparse table instead of between array, right?
Exactly. Sorry for omitting that detail
Thanks for noticing this, updated the post.
And why is it α(N)? It is log* n, I think (link)
You're right. I mistakenly used the notation. I updated my comment so that now it's correct
Implemented https://ideone.com/1yoW91 your approach for this problem https://leetcode.com/problems/shortest-subarray-with-or-at-least-k-i/
But that is O(log* N) assuming that sparse tables on each level are of size O(N), but if we'll find T(N) — pre-processing time of sparse table summary for whole array and make sparse table of size T(N) / (number of levels) for each layer not O(N)? Would it be closer to O(alpha(N)), where alpha(N) is an inverse Ackerman's function?? Or that would be still O(log* N)?
i didn't understand this : Each block size is a power of two. All the blocks are equal on each layer.
suppose if we added x zeroes and made our array an even power of two and then at next level it may happen that we need to add zero again and in that case array become discontinuous(as we need to introduce zero in middle way). so, how to avoid this.
I know i am missing something please help.
Suppose we have an array with size 211 = 2048.
Let the block size will be not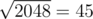 , but the nearest power of two: 26 = 64. So we will have 25 = 32 blocks.
, but the nearest power of two: 26 = 64. So we will have 25 = 32 blocks.
Because the block size is no more than 2·sqrt{n}, the asymptotic for block size remains , so all the time asymptotics remain the same.
, so all the time asymptotics remain the same.
What if instead of the between array or a sparse table we recursively use your structure on the blocks?
We can achieve a better complexity, though it will be harder to implement.
See the paper described in the comment by Rafbill.
Auto comment: topic has been updated by gepardo (previous revision, new revision, compare).
Thank you for sharing this idea and for clear explanation.