Hi! Topcoder SRM 730 will happen soon.
Time: 7:00am EDT Tuesday, February 20, 2018
Calendar: https://www.topcoder.com/community/events/
I'm the writer of this round. Hope to see you all participate!
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 148 |
| 9 | pajenegod | 145 |
| 10 | orz | 144 |
Hi! Topcoder SRM 730 will happen soon.
Time: 7:00am EDT Tuesday, February 20, 2018
Calendar: https://www.topcoder.com/community/events/
I'm the writer of this round. Hope to see you all participate!
| Name |
|---|



Reminder: The contest starts in 4 hours! Both SRM 730 and Humblefool Cup Qualifier's registeration has started!
Note that registeration ends in 5 minutes before the contest. Don't miss!
There is some kind of 'reward' survey when I'm trying to register this round. I did not participated in SRM 722, 723, 724, 726 and not interested in 'a chance to be recognized by the Harvard-NASA Tournament Lab and Topcoder' (btw, what does 'recognized' here mean?), but the survey asked me to select one of three. What should I do?
idk, but all I got was a sticker :)
+1 (also just got a sticker)
Do you mean on your topcoder profile or it was mailed to you?
It was mailed to me.
Hope you enjoyed the round! Here is some example code and some short explanations.
This invovles some casework. To make things easier, let's assume that x1 <= x2 to reduce the number of cases we need to consider. See the example code for details
This can be solved with dp or some combinatorics. For the combinatorics approach, fix the minimum as k. Then, the number of ways to choose the remaining numbers is (n-k choose x-1) Thus, the desired value is sum of k from 1 to n of (n-k choose x-1) * 2^k / (n choose x)
We use dp to solve this. Let dp[i] be the minimum max weight of stones we see to get a stone in node i.
dp[leaf] is easy to compute, as it is just the weight of the leaves.
dp[i] depends on the order that we choose to put stones on the children. Since weights are non-decreasing, it is always optimal to "pull" a stone all the way to a child and leave it there before moving on to processing a different child.
For each child, we have two values dp[c], the weight needed to get a stone on child c, and w[c], the weight that the child will need to hold while processing other subtrees.
If we order the children from as p_1, p_2, ..., p_n, we incur a cost of max(dp[p_1], w[p_1] + dp[p_2], w[p_1] + w[p_2] + dp[p_3], ..., w[p_1] + w[p_2] + ... + w[p_(n-1)] + dp[p_n]), and we want to minimize this value over all permutations.
By an exchange argument, you can show that sorting the children by w[c] — dp[c] gives an optimal permutation.
See div2 hard for a harder version on a non-binary tree.
For this version, we can try both orders for children.
There are a lot of different solutions, but they probably all start similarly.
Construct an independent set and a clique with k nodes. These are both necessary (and they can share at most one node in common, but given the constraints, you didn't need to share nodes).
My solution is to connect the i-th node in the independent set with the 1,2,...,i-th node in the clique.
Constructing the groups can be done in many different ways. In the solution I attached, I did some hill climbing to find all valid groups.
It's tempting to solve this by bashing on some sums (maybe it's also fast too...), but there are some simple combinatoric arguments that can get you an even faster solution.
Let’s consider the following situation. I have two bags, one with p balls and the other with q balls. I repeat the following step until one of the bags is empty. Choose a bag uniformly at random, and discard a ball from that bag. Let’s consider the distribution of number of balls in the other bag at the end of this process. There are two cases: either the first bag gets empty first or the second one gets empty first. If you write these two distributions down, you should be able to see a similarity to the terms one of the sums that we want to evaluate. You can also note the sum of these two distributions must be 1, so evaluating the sum can be done in x steps rather than n-x steps.
For each subset of {1,2,..,n} of size at least x, we can associate this with the value of the x-th largest element and group them together. The number of elements that are grouped at value S is equal to 2^(S-1), so we can see this problem is equivalent to counting the number of subsets of size at least x from {1,2,..,n}.
Challenge: Try to solve this for other powers that are not 2
"By an exchange argument, you can show that sorting the children by w[p] — dp[p] gives an optimal permutation." -Div2Hard
Can you explain this?
This may help
Easier combinatoric interpretation:
Let's look at all subsets of x or more elements and leave only x largest elements in each subset. Now each subset S of x elements appears exactly 2min(S) - 1 times.
So the answer is 2·sumi = xnC(n, i), which is easy to count.
I solved Div1 500pts in (probably) different way:
Let's think about the following sub-problem:
You are given N and K (0 ≤ K ≤ C(N + 1, 2)). Find one subset of (1, 2, 3, 4, ..., N) so that the sum will be exactly K.
This problem can be solved in greedy way, that does following operation in order of i = N, N - 1, N - 2, ..., 1. The operation is "If K ≥ i, select i from set and decrease K by i.
So, this problem can solve in O(N) time complexity.
Going back to the main problem, graph has edge (i, j) if and only if i ≠ j and i + j < n. And the "selection" is, you can restrict to selecting "either vertex k or vertex 2n - k - 1 (not both)". Let this vertex, "level-k" vertex.
Suppose that you select from level-n - 1, n - 2, n - 3, ..., 0 vertex in preceding order. If you select k in level-k, the number of edges on subgraph increases by n - k - 1, and if you select n - k - 1 the number of edges doesn't change. So, you can choose arbitrary subset of level 1, 2, 3, 4, ..., n, and the "increase value" of number of edges is (n - 1, n - 2, n - 3, ..., 0). This is equivalent to the sub-problem, which N = n - 1, K = x.
So this problem can be solved in O(N3), which is equivalent to output size, and the implementation is pretty easy (practically 17 lines):
Another solution for div1 1000:
f(n, x) is of the form 2n + 1 - Px(n), where Px(n) is some polynomial of degree x - 1, and Px(i) = 2i + 1 for all i < x.
Proof:
f(n, 1) = 2n + 1 - 2
Yes! In this way we can solve for any power. I see we need compute a sum like: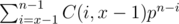 . And I guess that sum is a polynomial of degree x - 1 plus
. And I guess that sum is a polynomial of degree x - 1 plus 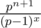 .
.
Do you have any proof for this?
Since you guess out it, it is not hard to proof. Just do an induction from recurence formula: f(x, n) = f(x, n - 1) + f(x - 1, n - 1).
It is clearly true for x = 1.
We can now use induction. For x > 1, If it is true for x - 1,
=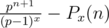 (by rearranging some terms, and using
(by rearranging some terms, and using 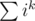 is a polynomial of degree k + 1)
is a polynomial of degree k + 1)
Did you expect d1 hard to be hard? (It wasn't even 900).
I didn't expect it to be hard, but it seems we forgot to adjust points accordingly (I had prepared this round a few weeks ago, so it wasn't at the top of my mind until a few days ago).
The testers didn't find a combinatoric interpretation at first (and one solved it for general powers first). I believe it can be easy to miss, but it also seems obvious after the fact. I briefly considered changing the power so it's not 2 which would have made it significantly harder, but decided it's better to let some of these easier solutions pass also rather than get almost no solves.
Div2Hard:
I guess it's just a typo, but in the problem statement it says that weights are "non-decreasing". Or it depends on which direction you look at the tree — bottom-up or vice versa :)
Update: another typo seems to be
dp[c], looks like you meantdp[i]instead.Fixed
A question unrelated to this round in particular -- why do the lower numbered rooms have more red participants than higher numbered rooms? Is it intentional and "fair"? I'd expect that hacking in a room with 50% red is much more difficult, as higher percentage of submissions is expected to be correct, and there are better and faster hackers.
As I understand first coders are distributed randomly and then rooms are ordered based on strength
When I was the admin, there were a few algorithms for room assignment. In SRM it was named "Random Seeding", in TCO it was named "Ultra Random Seeding", though I don't know details.
It used to be the case that they only used actual uniform random for rounds that had monetary prizes (TCO, sponsored SRMs). For regular SRMs they used some biased algorithm that made it more likely for higher-rated coders to end up in lower-numbered rooms. This was intentional.
Given that nowadays TC doesn't really care about their Algorithm track, I'm quite sure this is still the case, and that these are the two seeding algorithms [h]rng_58[/h] mentions.
(I don't know why they decided to use the biased seeding algorithm. It's not completely fair, but at the same time the bias isn't large enough, so the contestants never complained too loudly about it, I guess.)
majk is complaining. I was also complaining when I found myself in the room 1, with Petr and a bunch of reds. The rest was yellows and 2 blues.
However it is also not completely true, that this is such a disadvantage. If the tasks are difficult, quite often lower rated coders do not submit anything, whilst higher rated coders are more likely to submit a solution. Because the task is tricky/difficult, there is also a higher chance for them to make a mistake, so I started to wonder, whether my complains were reasonable.
In SRM 729 it was quite fortunate situation for uwi, who managed to win the SRM because of lot of wrong solutions in my room and his excellent speed and solid preparation in the coding phase (and my inability to stop thinking about the hard task and concentrate on the challenges :-)).
The complaints are not unfounded, though. However, I doubt that they will change anything, since I also have the feeling that the algorithm track lacks a bit of love from TC staff. Case in point, the time in the web arena is still off by 4 hours.