E: I assumed that the answer is either at most N or infinity. Why is this true?
G: Is there a solution that doesn't require reading papers (or at least reading the wikipedia article mentioned in the statement)? I heard that there's a paper that describes the solution.











E: Because if rank doesn't drop at some point it never drops again. This is true because if im(Ak) = im(Ak + 1) then this image stabilizes. Moreover I was convinced that all this task is about is how to sped it up from obvious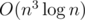 to tricky O(n3) by taking random vector and computing Ak v, was disappointed.
to tricky O(n3) by taking random vector and computing Ak v, was disappointed.
Can you please explain a bit more how to make this speed up?
I already more or less described it. You take random vector v and compute Av, A2v, A3v, ..., Anv and output smallest k such that Akv = 0 or Infinity if Anv ≠ 0
Okay, thank you, now I understand your approach
We were able to get accepted by simply optimizing the O(n^3 log n) approach.
Yes, that was what I was talking about, that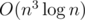 was actually passing quite easily.
was actually passing quite easily.
What is the proof for "image stabilizes" fact? Specially, when we are working in mod prime?
It's due to the fact, that im(Ak) is a subset of im(Ak - 1). So if im(Ak) = im(Ak - 1), than for each v in im(Ak) there is an u such that Au = v and u is in im(Ak - 1) = im(Ak). And this means, that v is in im(Ak + 1) too. So im(Ak + 1) is a subset of im(Ak). QED.
Yes, that I get it. I mean, if C = A*B, then columns of C are linear combination of the columns of A. But I was wondering, why the modulo operation does not knock some vector off? I mean, why it's also true when doing modulo operation.
Well, i haven't used anything connected with the field I am working in. Everything I've said is also true in Zp
Problem G can be solved in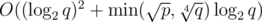 (if you assume, that arithmetic operations work in O(1)). You should use Adleman-Manders-Miller root extraction method (I don't see any difference between this method and Tonelli-Shanks). This article contains a good description of the algorithm. Additionally, you should modify their method, so that it has better complexity. In order to do that, you should use baby-step-giant-step instead of brute-force in the last part of the solution.
(if you assume, that arithmetic operations work in O(1)). You should use Adleman-Manders-Miller root extraction method (I don't see any difference between this method and Tonelli-Shanks). This article contains a good description of the algorithm. Additionally, you should modify their method, so that it has better complexity. In order to do that, you should use baby-step-giant-step instead of brute-force in the last part of the solution.
I guess, that teams, who have solved this problem, knew Tonelli-Shanks before the contest or read the article in Wikipedia.
Yes, it's not really a new problem, I'm sorry for that. But Tonelli-Shanks is actually pretty simple, and I want it to become more well-known.
There is additional trick here. We can't use baby step giant step as a blackbox. We need to use fact that we know that our result will be small, so that even though it is modulo q, it works in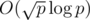 (because p is upper bound on result we are searching for in this moment) instead of usual
(because p is upper bound on result we are searching for in this moment) instead of usual 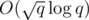 (and we know p can be upper bounded by 109 because cases when
(and we know p can be upper bounded by 109 because cases when 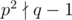 are easy (this is where this
are easy (this is where this 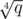 comes from, because we can bound
comes from, because we can bound 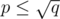 and then we solve BSGS in
and then we solve BSGS in 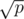 ))
))
Btw, I don't think that Tonelli-Shanks is pretty simple xD
Does anynody have a rather clean approach that they’re proud of for problem Oddosort? Or at least something that could be written rather quickly?
Well, I think our is quite ok.
It's quite easy to get a range that is non-decreasing. Let's do a big loop, inside which do following. In another Get next two such ranges, and merge them. If one left, to nothing with it. If only one left total we are already won.
The only problem we had, is we wrote solution for <=, not <, and got problems with stability.
That solution is O(n2) on decreasing arrays, isn’t it?
During the contest we thought that intended solution was O(nlog(n)), so we implemented a variation of merge sort. It’s pretty embarassing if O(n2) fits no problem.
No, it's not. You probably understand that we get first two blocks, but we are scanning array and merge 1 and 2 block, 3 and 4-th, and etc. This works nlogn, because number of blocks is divided by two every time.
It's the official solution. I wrote a program in C++ first and then used some
sedscripts to convert it to Meow++ (removing brackets, comments, debug function calls, etc). That allowed me to debug conveniently using all standard tools.You can do a mergesort. There are only 18 levels of recursion which can be emulated by 18 (identical except for variables) nested loops.
How to solve A?
Let's consider the image on a 2D plane. Now assuming that upper right corner is on (2^k, 2^k) and lower left corner is on (0, 0). We can do recursion to assign coordinate to each square. It would be like this:
go(x1, y1, x2, y2):
int x;
cin >> x;
if x == 1:
squares.add({ x1, y1, x2, y2 });
if x == 2:
go(x1, (y1 + y2) / 2, (x1 + x2) / 2, y2);
go((x1 + x2) / 2, (y1 + y2) / 2, x2, y2);
go(...);
go(...);
Now we can iterate over the squares and check whether it connected with some previous squares or not. So we have a graph and there we need to find the number of connected components (we can use DSU instead of storing whole graph in memory).
But the problem is that 2^k is really large to store this number in a long long variable. We can create struct to store coordinates is a binary representation (storing only powers).
https://ideone.com/7ZgrFU
O(n3)?
I wasn't able to come up with faster approach. I guess it can be proved that it works in O(n2) time.
We solved it differently: For every square store 8 pointers (4 for squares inside), and 4 for adjacent squares that are bigger. We can maintain this data just by doing dfs/bfs + using dsu for simplicity. It is O(n).
Can be done with the same idea even without DFS/BFS — just merge neighbouring black blocks with DSU.
Was B just accurate brute-force with backtracking?
Backtracking was one possibility, you could also for every triplet of pieces (with order) and all their rotations, reflections and displacements try to create a corner, compute the border of the corner and check whether there is a matching corner from the other three pieces.
Meet-in-the-middle! Smart, thanks!
How to solve problem C?