Hello everybody,
Recently, while exploring vjudge, I came across this problem and I have no idea how to solve it.
Basically, we are given N points (N ≤ 1000), no three points lie on the same line, and we are to find the sum of areas of the convex hulls for each subset of at least 3 points. There are multiple test cases and the sum of the N values over all test cases is up to 5000.
Can anybody share some ideas about this problem, please?











In the popular algorithm for computing area of a polygon with cross-products, we take advantage of the fact that one can calculate the "area" (actually integral) independently for every edge and then sum them to get the total area.
There are O(N^2) possible edges in any convex hull. To be able to use the polygon area algorithm on this problem to calculate the contribution of a given edge in clockwise orientation, you need to be able to calculate two things: its integral (easy) and the number of convex hulls it is a part of (little bit harder).
For the second part, think about what the condition is for an edge to be a part of a convex hull. After that it should become obvious how to count how many times that edge shows up in one.
Wow, I never realized that this formula was actually sum of integrals :D Thank you very much! Got accepted, here is the code in case somebody is interested.
Probably the same solution as the one mentioned by hex539 but explained with details:
Fix two points. The segment between these two points will be a part of some number of hulls. To count them, we first notice that this segment may be both clockwise or counterclockwise oriented. If the orientation is clockwise, we can draw a line through these two points and count the number of points above the line. Let this number be C. Then the number of convex hulls in which this segment appears in clockwise direction is 2C - 1. Similarly it appears in counterclockwise direction 2N - C - 2 - 1 times. From here we get an obvious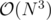 solution.
solution.
To get a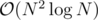 solution, we first fix a point and sort every by angle with the fixed one. Well now we simply have to do a sweep line algorithm, keeping two pointers. There probably is a smarter solution but this should work.
solution, we first fix a point and sort every by angle with the fixed one. Well now we simply have to do a sweep line algorithm, keeping two pointers. There probably is a smarter solution but this should work.