There are many 2D rectangles in 2D space. Given a point, suppose this point did not hit (inside of) any rectangle, find the one rectangle it is closest to. Assume the rectangles are not rotated. Can it be faster than O(n)?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 07:04:18 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I will kinda gloss over technical details for now, feel free to ask for clarifications.
I suppose that you want to answer queries of type "What is the closest rectangle to this point?" in less than O(n) time. Now shortest distance from the point P to the rectangle is the shortest distance from the P to one of its sides. The shortest distance from P to the segment AB is either min (|PA|, |PB|) or length of perpendicular from P towards AB, if it lands on the segment AB of course.
Now, let's see which case actually happens for rectangle, which is the closest to the point P. Dealing with second case is simple: we just need to cast 4 rays in all coordinate directions from the point P, for each ray find the first rectangle they intersect and remin answer with this rectangles (note that because all rectangles are axis-parrallel, all perpendiculars to the sides are axis-parallel too). To deal with the first case, you need to find the closest point to P among the corners of rectangles: in general, such a problem can be solved with Voronoi diagram (and I am pretty sure that there is not anything significantly simplier in general case), in your case there may be some simpler solution, but I can't see it for now.
Total time: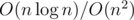 precalculation (for Voronoi diagram),
precalculation (for Voronoi diagram),  per query. It seems that you need something like a persistent treap to answer queries online, but offline you can do a scanline with set to handle both described cases (after you built the Voronoi diagram, of course)).
per query. It seems that you need something like a persistent treap to answer queries online, but offline you can do a scanline with set to handle both described cases (after you built the Voronoi diagram, of course)).