I was interested in this problem in GCJ Finals and thought of its general case (= the board size is infinite).
Rule
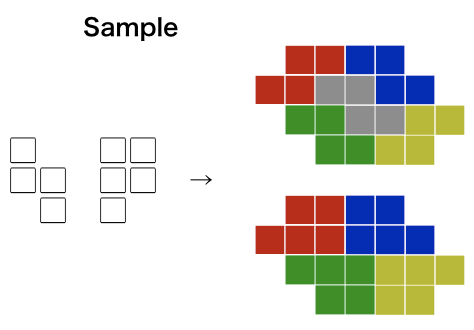
You are given two (or more) type of polyominoes. Find a shape satisfies the condition "can be filled completely with some number of polyominoes of the same type in no overlaps" for each type of polyomino.
A shape with fewer cells is considered better but it's not necessary to minimize.
Sample
Problems
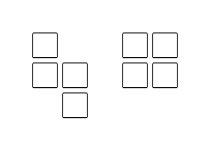
(1)
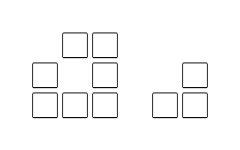
(2)
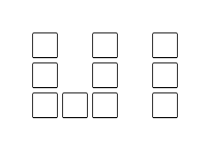
(3)
(4)
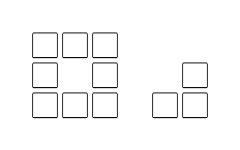
(5)
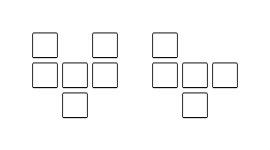
(6)
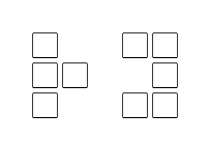
(7)
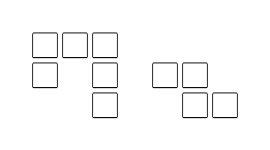
(8)
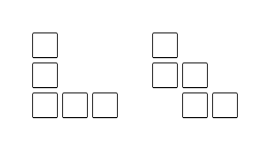
(9)
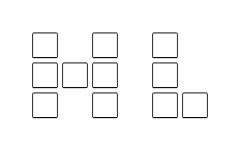
(10)
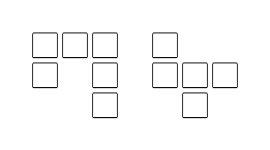
(ex)
I welcome your solutions or new problems!



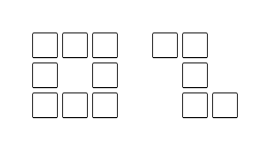








The thing you are referring to is called "least common multiple of polyominoes", some known results in this field are google-able.
Thanks! That's a keyword exactly I wanted to know. However I googled and got no result for exact phrase and few results for polyominoes or LCM. Was my use of google something wrong?
Indeed, looks like there are not so many results for "least common multiple of polyominoes", http://www.paulsalomon.com/uploads/2/8/3/3/28331113/polyomino_number_theory_(i).pdf was the second link after Wikipedia for me and I assumed there should be more. On the other hand, this article mentions another term that gives more results for me:
Oh, I missed it. I could get many result for "compatible polyominoes" e.g. this wonderful study. Thank you:)
This site and this site contain a lot solutions, including to most problems you gave.
Thank you. Wow, there were so many works than I expected! I'll view these pages all day long:D I was surprised that the solution for O4-T5 is very complex.