[](https://open.kattis.com/contests/asiasg18-prelim-open/standings) How to solve D and E, I tried but failed.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3650 |
| 2 | Benq | 3582 |
| 3 | Geothermal | 3570 |
| 3 | orzdevinwang | 3570 |
| 5 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3532 |
| 8 | Radewoosh | 3522 |
| 9 | Um_nik | 3483 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/23/2024 15:55:15 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










D: Find all bridge in the graph, then DFS to see how many vertices reachable from vertex 0 after removing all the bridge.
E: Binary search the answer. Suppose we need to check whether it is possible to find a combination of N numbers with the minimum not less than X. Build a bipartite graph where vertices on the left represent row, and vertices on the right represent column. For each cell ai, j, if ai, j ≥ X, connect an edge from i-th vertices on the left to j-th vertices on the right. If the maximum matching of the bipartite graph consist N edges, it is possible to find a combination of N numbers satisfying the condition above (we choose all cell (i, j) such that the edge connecting i-th vertices on the left and j-th vertices on the right is in the maximum matching).
Anyway, can anyone explain G and J?
G: precalculate all N such that Bob will win. There are only less than 400 such values. You need an efficient enough precalculate program. Ours runs in less than 10 minutes.
How did you precalculate these N efficiently?
For each i<=10^9, determine if there is any N found so far such that i-N+1 is prime. If none of them is, i is a new N we found.
Can you prove an upper bound on how many i from 1 to N that Bob will win?
No, I guess it's related to distribution of primes which is really complicated. In contest, I discovered there are really few N that Bob will win only by experiment.
If someone is interested.
My offline sol to find all possible nos.
And AC soln with all no hardcoded.
But I as of now I don't have any proof on the upper bound.
Unable to solve A with DFS? I tried but got TLE, so I changed to an algorithm O(9*n^4).
My Soln of A.
Can you share yours?
Here
Thanks. You can reduce your time complexity to O(9*8*n^2). By using this piece of code.
J:
The first part can be computed by a O(2VV2) TSP DP. The overall time complexity is O(2VV3) since you need to compute at most 2V times Gaussian elimination.
Do you know any tutorial on how to compute determinant of a N * N matrix in O(N3)?
After applying Gaussian elimination in O(N3), the determinant of the matrix is equal to the product of all the element on the main diagonal.
how to solve F?
My soln for F -
Chose a const SIZE ~ sqrt(n). (500 gives AC, and 1500 gives TLE on last TC) Now divide all B into two half one less than SIZE and other greater than or equal to SIZE.
For Type 1 queries - if B > = SIZE. Directly update all values. //O(n/SIZE) if B < SIZE, //O(1) Keep an array inc[SIZE][SIZE] i.e. (B,A)
And update as inc[b][a] + = cst
For Type 2 queries -
Time Complexity — O(Q*SIZE) in worst cases.
But unfortunately, it gives AC.
Can I see your full code? send it for me to this email thanks. [email protected]
Link of code is already present in the comment. Just click on soln in first line. :P
How to solve C, H, I?
C: Dynamic Programming. Consider building the big string (I'll call it T) character by character. Because it has to be a palindrome, when we assign T[0], we also assign T[2N - 1]. Keep a pointer to the head and tail of S. When we assign positions in T, we may need to move the head and tail pointers of S. When S is a subsequence of the prefix / suffix of T that we've built so far, just multiply by 26remaining. The state is just how many characters are remaining and the positions of the pointers in S for a O(n3) solution.
H: Just BFS from outside the grid and count how many walls you hit. If you enter an "active" cell don't continue the BFS from there.
I: It looks like finding the coefficient of xk in (1 + x + x2 + ... + xm)n. No idea how to do that efficiently.
I is a pretty standard problem. For example, see 451E - Devu and Flowers for the application of the same idea.
Firstly, consider the case when m (the number of objects of each type) is infinite. In this case the answer is simply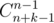 (you need to count ways of splitting k in n non-negative integer summands; that is the same as splitting n + k in n positive integer summands; that is the same as splitting n + k balls lying in a row in n non-empty groups by placing n - 1 "walls" that separate the groups in n + k - 1 positions (between each pair of balls)).
(you need to count ways of splitting k in n non-negative integer summands; that is the same as splitting n + k in n positive integer summands; that is the same as splitting n + k balls lying in a row in n non-empty groups by placing n - 1 "walls" that separate the groups in n + k - 1 positions (between each pair of balls)).
But we overcounted something: we counted the partitions of k in n non-negative summands where some summands are larger than m, though we should have not done that. Let's use inclusion-exclusion to handle the overcounting.
How many partitions of k in n non-negative summands there are, if we are required to make some i fixed summands larger than m? Let's note that there are as many of them as there are partitions of k - (m + 1)i in n non-negative summands (simply subtract m + 1 from each "definitely overflowing" summand, after that there will be no restrictions on said summand).
In the end, by inclusion-exclusion, the answer is equal to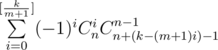 (we need to choose i definitely overflowing summands out of n and count the partitions of k into n summands such that i of them are definitely overflowing).
(we need to choose i definitely overflowing summands out of n and count the partitions of k into n summands such that i of them are definitely overflowing).
Does there any way to solve this problem with polynomial multiplication?
For I, we can rewrite the expression as (1 - xm + 1)n(1 - x) - n. Just use the binomial expansion on both and you have to evaluate the following:
I do not really understand the solution for C.
"Because it has to be a palindrome, when we assign T[0], we also assign T[0]." Do you mean T[0] and T[2*N-1]?
How do you handle S being in the middle (i.e. it does not lie entirely in the first N letters or the last N letters) for the DP state? I do not see how the transitions work for this case.
EDIT: I misread the question as substring instead of subsequence, so the solution makes a lot more sense now...