The 2018 Egyptian Collegiate Programming Contest was held yesterday this was a problem from it where he asks for

Where n<=10^5 and a[i]<=10^5 answer should be printed %10^9+7
I would appreciate any help in solving this problem and thanks in advance
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 7 | SecondThread | 150 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
The 2018 Egyptian Collegiate Programming Contest was held yesterday this was a problem from it where he asks for

Where n<=10^5 and a[i]<=10^5 answer should be printed %10^9+7
I would appreciate any help in solving this problem and thanks in advance
| Name |
|---|



inclusion exclusion
For a fixed g how many pairs that will have this g as a gcd, it'll be all multiples of g, it's easy to get the sum of multiplying those pairs.
but there is a problem with this, there will be some pairs that will be calculated multiple times, so we have to exclude the answer of (2 * g, 3 * g, ...), for example if we are solving when g = 2 we know that all the numbers divisible by 4 is also divisible by 2, so we have to exclude the answer of 4, and so on.
so the answer is iterate from the max number in descending order to 1 and solve for each fixed g, the total complexity of this solution is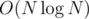
Mhm... nice problem. Do you agree, mnbvmar?
<3
Story: We proposed this exact task (under a tiny bit different constraints, though) to our high school students back in 2015. I was quite surprised that apparently it has never appeared anywhere even though the statement feels really natural and obvious. So it seems it eventually did!
I think tribute_to_Ukraine_2022 came up with another solution, involving...
the Möbius inversion formula
I can't remember any details, though. Mind sharing (if you still remember it)?
First I calculated an array B[n] such, that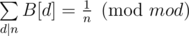 (how: first set
(how: first set 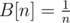 , then for each i from 1 to n iterate over all multiples of i and subtract B[i] from B[di]).
, then for each i from 1 to n iterate over all multiples of i and subtract B[i] from B[di]).
Now we can just iterate over all possible d and add to accumulator sum of entries divisible by d squared times B[d]. This way for each pair a[i], a[j] we have added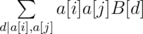 , which is equal to
, which is equal to 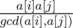
The only moment where Möbius inversion formula came into play was calculating B[n] array. It can also be done using that formula, but the way I posted here is much easier. I think i used this approach on that contest back in 2015, but I'm not sure
Can anyone tell me why my solution gives TLE.
If I am analysing time complexity properly, my code should take $$$O(n + max(a_i)*log(max(a_i)))$$$ time per test case.
Submission : 111169206