For today's Div 1 problem D, 1067D - Computer Game, once you succeed at a quest, it's clear you should upgrade and play the quest that maximizes your expected reward pi × bi for the remainder of the game.
However, before you succeed at a quest, you have a difficult tradeoff to make: should you take a quest with a high probability of succeeding, to maximize your chances of upgrading and gaining optimal points for the rest of the game? Or should you take a quest that gives you more expected reward pi × ai right now?
It turns out the answer to this tradeoff depends on T, the number of seconds left. As T gets smaller, we should switch to quests with lower pi but higher immediate reward pi × ai. This is because the long-term value of upgrading and maximizing future rewards becomes less relevant compared to getting more reward now. In particular, the optimal quest to pick (when we have not yet succeeded at any) can change multiple times as T gets smaller and smaller. My solution 44819755 uses multiple binary searches along with a stack to determine the optimal switching points.
Unfortunately, the system tests are extremely weak at testing this logic. Many competitors submitted solutions that never even choose to switch quests. This actually passes all of test cases 1 through 104. It will only fail on test case 105, the very last test case, where ironically N = 2:
2 10
1000 1001 0.1
10 1000 0.5
In this case, except when T = 1 you should always perform the second quest, as this gives you a 50% chance of upgrading and getting 0.5 × 1000 = 500 expected reward every turn thereafter. However, when T = 1, upgrading has no more value, so you should perform the first quest instead for an expected reward of 0.1 × 1000 = 100, as opposed to the second which only gives 0.5 × 10 = 5 immediate reward. So this test case requires just one quest switch at the very end.
This case was enough to catch the majority of wrong submissions. However, since it's very simple, it was still possible for incorrect solutions to get through. In-contest, I believe only one did: 44804123. In particular here is a case where two switches are required:
3 3
3 4 0.5
6 25 0.4
15 16 0.2
The maximum pi × bi here is 0.4 × 25 = 10, which is the amount we will get each turn after succeeding and upgrading.
When T = 1, we should choose quest 3 for an immediate reward of 0.2 × 15 = 3, the maximum possible.
However when T = 2, we should choose quest 2, which gives us an expected value of 0.4 × (6 + 10) + 0.6 × 3 = 8.2. Choosing quest 3 only gives us 0.2 × (15 + 10) + 0.8 × 3 = 7.4. Similarly, choosing quest 1 only gives us 8 points.
When T = 3, we should actually choose quest 1, which gives us an EV of 0.5 × (3 + 2·10) + 0.5 × 8.2 = 15.6. This is higher than choosing quest 2, which gives us 0.4 × (6 + 2·10) + 0.6 × 8.2 = 15.32.
So the answer for this test case is 15.6. However bazsi700's Accepted solution above outputs 15.5 because it never uses quest 2.
If you're working on this problem in practice mode and want to know whether you actually solved it, make sure to test the case above and a few others like it!











I really think that Um_nik should stop creating problems.
What if he didn't have enough time for tests? What if he was too busy judging other authors problem setting abilities?
Sick burn.
I have to say, ignoring this issue I liked the problem quite a lot! And luckily test 105 ended up mostly saving the day.
Though I will say that I wish it had been worth more points than problem E ;)
Do you think only the tests were weak, or his mind as well?
Is there exists a test with a big value of T (more than 105) on which greedy solution doesn't work? Because if no, then we can write simple dynamic programming solution in O(T·N) or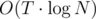 for small T, and greedy solution which never switches for large T.
for small T, and greedy solution which never switches for large T.
I guess it's such a test:
2 10000000000
10000 20007 0.000000001
3 3 0.000000002
Are you sure?
The greedy solution gives 190069.500020, while the correct solution gives 190069.507940. The relative error between these two numbers is 0.0000000415, which is less than 10 - 6.
I tried neal's submission, and it says we should switch after 100M turns.
Which greedy solution you try? I checked your submission from contest and it gives wrong answer: https://ideone.com/uGRQ0N
Ok, check please following test:
2 1000000000
100 180 0.000000001
30 30 0.000000002
It's because of %I64d in my solution. Ideone uses Linux OS, so you should change %I64d to %lld in the scanf. With %lld my solution gives the correct answer: https://ideone.com/DqziP6.
New test really breaks a greedy solution, thank you!
Thanks for the information. It's pretty saddening that this case wasn't included in the 100+ tests. Sometimes weak pretests bring me down, now weak system tests bring me up.
To be fair, Um_nik did have a test that required switching quests 20,000 times; it just didn't make a difference bigger than 1e-6. Goes to show that if you want to break a wrong solution, you really have to implement the solution and make sure it fails.
This leads to a nice challenge though: what's the highest number of mandatory quest switches you can fit into a test case? (i.e., choosing to use fewer quest switches leads to the answer being wrong by more than 1e-6) Bonus points for making T large in order to break various slower solutions. Looks like MrDindows already has a good start.
Here's what I've got -- a test case where N = 729 and T = 6 million: https://pastebin.com/remMhWv6
The correct answer is 1456388.705926. If you make use of any fewer than 400 out of the 729 quests, you can get at most 1456362 points (relative error of 2e-5).
Um_nik, can you add this test and MrDindows's second test above to the system tests in practice mode?
Update on this: the system tests in practice mode have been strengthened with several of these tests.
Wrong answer on test 106: http://codeforces.com/contest/1067/submission/44927156
Accepted after 110 tests: http://codeforces.com/contest/1067/submission/44927930
I'm trying to see if it's also possible to rejudge the existing Accepted solutions (practice mode only, of course). Thanks to kristevalex for taking time to help out with this!
I've already rejudged them.
Thanks! I've added everything from this blog to the tests, (of course, there will be no rejudge of contest submissions). Feel free to write if you will come up with new helpful testcases ;)
Official standings were also affected by the rejudge. If you go to the profile of bazsi700 you can see that he was theoretically 19'th and when you go to the standings, you can see he was 61'st.