Pre-Elimination round of SnackDown will take place today.
But I can't understand the rules with Judging Criteria, how they will sort the teams with equal number of tasks (or points).
On the page of round it is written (Link):
Users are ranked according to the most problems solved. Ties will be broken by the total time for each user in ascending order of time.
However, on the page of the SnackDown2019 it is written (Link):
The qualification & pre-elimination rounds will use score based ranking system.
And if we go by the link, what it is score based ranking system, we get ( Link )
The ties are unresolved. The time elapsed is not considered.
So we have contradiction in the rules, what the rules will be used in the contest? It is good to know it before that start of the contest.











I think it is with high probability they will use ACM ICPC rules. I dont know if the penalty will be 20 mins or it will be changed.
Adding PraveenDhinwa. he should be capable of answering.
The contest's page says 10 minutes per penalty.
https://www.codechef.com/SNCKPE19
Is it allowed to use 2 computers during the round?
As there is basically no way to supervise it, I'd guess it is.
I think he meant parallel login to the same account using both PCs. It was allowed in all previous rounds so maybe it will be allowed in this also.
Isn't it enough to login with your personal profile and submit from there? I think it counts as a team submission then.
Yes, it's enough.
Yes, it's allowed.
From the announcements section of the contest: "16:30 IST, 3 Nov: Teams will be ranked according to number of problems solved. Ties will be broken according to ACM Rules, but with a penalty of 10 minutes for each unsuccessful submission."
How to solve Strange Transform?
Solution of my teammate: use sqrt decomposition.
For K <= 2^9 calculate answer
For K <= 2^18: run recursion.
Total time ( n + q) * 2 ^ 9
Code
My solution is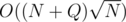 . If k is small, use
. If k is small, use 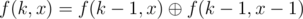 (precompute all such values with this formula). Otherwise use
(precompute all such values with this formula). Otherwise use 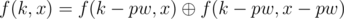 , where pw is the largest power of 2 which is not greater than k. Couldn't fix all bugs before the end of contest...
, where pw is the largest power of 2 which is not greater than k. Couldn't fix all bugs before the end of contest...
Note, that fk(a)x = xor over{j which is submask of k} a_{x+j}.
Note, that you can get k modulo 218 (implied by first statement)
Precalculate all fk(a) for k ≤ 29.
Now you are given k = l + m, where l is divisible by 29 (and therefore contains at most 9 bits) and m ≤ 29. Find fl(fm(a))x. fm(a) is precalculated and finding the rest can be done by enumerating submasks in 29.
Overall complexity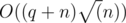
How to prove the first observation?
I only know that it is related to the parities in Pascal triangle.
edit: It is easy to be proved by M.I. but is there some more intuitive way to reach this conclusion, other than pattern observation?
First you should notice is each one has binomial coefficients. And later we need coefficients mod2 so whem we apply Lucas thoerem, we get that observation that r must be submask of n for nCr to be odd.
First proof how f2 works, then how f2k works (by induction). Then it's easier to see
When upsolving usually becomes available?
UPD: now it works
How to solve Painting Tree ?
At first let's calculate fk — number of ways to choose k non-intersecting paths.
With this + some simple combinatorics you can get the answer.
Isn't trivial dp to compute fk is O(n^3)? Although it's not that trivial!
I don't know whether we about the same dp, but there's is pretty straightfowrard one and it's O(n^2) because in each vertex it's not O(n^2) but O(left_size * right_size) which is O(n^2) in total.
Same trick used in the Polish problem Barricades (see Looking For A Challenge) reduces it to O(n2).
I think that a part of the statement of QUEENS was misleading:
Let's denote a unit square in row r and column c by (r,c). Chef lives at square (X,Y) of this chessboard.Here y-coordinate is denoted by X and x-coordinate by Y. Yes, the statement is technically correct, but the choice of variables is against the common conventions. Was this an oversight or an intentional attempt to mislead contestants?
the only reasonable choice of order, imho.
Matrix conventions are different from the 2D cartesian plane conventions. According to convention in a matrix, rows are numbered from 1 to n from top to bottom and columns from 1 to m from left to right.
Yes, the notation (row, column) was indeed correct. What I meant is that in the statement a variable called X was used to represent row (the "y-coordinate" in matrix) and Y to represent column ("x-coordinate"). In my opinion, the names of the variables X and Y should have been swapped.
That's my point. There isn't any concept of x-coordinate and y-coordinate in a matrix. As a row number is written first and when (X,Y) is being used to describe a pair, X is used to describe the first number, so it makes sense to denote row number by X and column number by Y. I am not saying you are wrong, just want you to see the other perspective.
As it usually goes, the first coordinate in an array is x, the second coordinate is y, the third is z and so on (or i, j, k and so on). Makes perfect sense unless you're programming in Befunge or Logo.
I remember a contest (Polish maybe?) where rows were y and columns were x. Boy, was that confusing.
Of course man, if you are referring to matrices coordinates by z and y you should do (y,x), not that freaking most confusing in world (x,y) for row and column. I don't care about whether x comes before y or not, I care about their meaning. x is left right and y is up down. If not necessary you should omit denoting matrices coordinates by x and y, but sometimes we think of our matrix as a map where some units are moving or whatever.
But it isn't (x, y) for row and column. It's (r, c) for row and column, right there in the statement. It's just that specific coordinates aren't also named r and c, they're named X and Y. If they were named A and B or Bacon and Popper, that wouldn't change the fact that which coordinate is the row and which is the column is explicitly spelled out precisely to make sure the statement explains such misunderstandings.
Perhaps not the best choice, sure, but I don't know what's the best choice and am not going to bother when I'm sick.
I agree that x and y shouldn't be used in grids, especially with x denoting row.
How to solve Heap Pirates?
I only know how to solve it when we have a bamboo (it's just a line of length n that looks like
010101).And the other case i know is the sun (graphs with edges like (1-2) (1-3) (1-4) ... (1-n)). For n=4 it looks like this:
1010100000Are there any other figures?
Yes, any tree is fine. Recursively run something like this: Group corresponding to root will cover left, right and bottom of its rectangle. Children will be placed in the top, skipping 1 cell. Think of a hairbrush
There is an answer for any tree. Root the tree and generalize your idea :)
what is the complexity for activity selection O(n^6) with small constant. or can it be done in better complexity ?
I did O(n^5), however it is pretty clumsy to describe :f. I would be disappointed if it turns out that O(n^6) was sufficient to solve this problem. Can somebody that tried to squeeze O(n^6) write here what was the outcome? My code is here: https://ideone.com/Qwtbse, but I am not sure whether it is of any help without some description :P
I just wrote straightforward n^6 solution and it passed right away
R u sure yours is n^6 because contraint on m was m <=50.
Yes. My solution is n^2km^3
Yes, unfortunately, some O(N6) solutions did pass, I apologize for this.
My solution was O(N4M) and it ran quite slow without any constant optimization, so I thought O(N6) solutions are not feasible. Lesson to learn from this is that a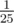 constant factor is actually quite achievable given the large variety of O(N6) solutions with small constant factors out there.
constant factor is actually quite achievable given the large variety of O(N6) solutions with small constant factors out there.
O(n^5)is quite straightforward.Let's use dynamic programming. We'll add intervals in an increasing order of their right border.
The state is
(last_right_border, current_k, current_k_pos, current_intervals_count). The value of the state is the number of ways to pick exactlycurrent_intervals_countintervals so that the current longest sequence of non-overlapping intervals has lengthcurrent_k, the leftmost of such sequences ends in thecurrent_k_posposition and we've considered all possible intervals that end inlast_right_borderor to the left from it.To make a transition, we iterate over the number of the intervals that end in the
last_right_border + 1position. Once this value is fixed, we've got two options: 1. The new intervals will not change the current value ofK(which means they start before thecurrent_k_pos). 2. They will increaseKby one. It means that at least one of them starts after thecurrent_k_pos. Either way, the number of ways to choose the new intervals is some binomial coefficient.By the way, this solution takes around half a second to complete in the worst case (I didn't do any constant optimization, though), so I don't think that an
O(n^6)solution can pass.I have troubles understanding how that is n^5. I think currentintervalscount is up to n^2, so you have dp table of n^5 size and as I think of it you need to have linear number of transitions from every state where you add those binomial coefficients. What am I missing here? Are you doing last step in more clever way?
The total number of intervals is up to 50 (according to the problem statement), so I counted it as
n.Oh no, FML... My solution runs in n^5 for M<=(n choose 2) though (I don't have M in complexity at all)
Lol, after this discussion I saw the question and realise its min(50,...). sad life :(
Anyways if possible give a brief description of your idea. no need of complete details
In kraskevich's solution he keeps track of how many intervals he chose and what is our current result on prefix. I call intervals contributing to result as important (k of them) and others unimportant (m-k of them). I do not decide when do I take unimportant intervals when doing transitions, I just count in how many places I could have put them and keep track of that (corresponding to variable 'luzne' in my code) and in the end I chose m-k out of luzne. Advantage of that is that I can optimize this by suffix sums because instead of adding some weird binomial coefficients I just add some fixed constant on some interval.
If my last important interval on some prefix ended at index e and I am considering adding intervals ending at i then I either:
1) chose not to increase result by not adding any interval [b, i] for b>e and then I have e places for unimportant intervals looking like [b, i] for b<=e
2) chose to increase result by adding some interval [b, i] for b>e (I look at one with biggest b) and then I have b-1 places for unimportant intervals
Trick is that I do not have to iterate over b in second case since this can be seen as adding constant on interval (b iterates from e+1 to i).
When you waste an hour not noticing that heaps can have 0 counters in
buddynim:(What about T-shirts?