I am stuck on this following problem:
Statement:
Given a string of size n and q queries of type (l,r) you need to find how many palindromes are there in the substring of range [l...r].
Constraints:
1<=n,q<=100000
1<=l<=r<=n
Thanks for reading the problem. It will be really helpful if you can give me a solution.











Mistake in approach.
Thanks for your reply.
But I am not clear about the merging procedure. Can you please tell me more about this part "number of palindromes between this parts (left end in first half and right in second)."
why even O((r - l) * logn)? You can preprocess string using Manachar's algorithm, and then for each i in [l, r], you can find the number of palindromes in between the parts, centered at i in O(1), so it's just O(r - l).
but I don't understand, how it will be O(nlog2n) in total, because you will have to merge even for queries. Can you please elaborate.
[deleted]
We know that there can be at most n palindromes in a string of size nNo there can be n2 palindromes, for example consider
aaaaaa.so that won't work :|
Sorry, you are right.
Mistake in approach.
"each interval will be smaller in at most logn merges"
No, you may even have to merge already merged intervals, with a simple interval. So that won't be O(nlogn)
You are absolutely right! I will try to invent something better and correct :)
Sqrt-decomposition solution is costly but may pass, depending on TL.
Whenever you add/remove some index, you have to add/remove palindromic substrings ending at that index, which you can find using binary search (hash the string and it's reverse).
Total complexity will be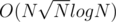
How will you find palindromic substrings ending at some index by binary search?
HashingHash the given string and it's reverse, Now you can binary search on the maximum length that can be a palindrome ending at that index (in the direction you want). To check if the substring of given length is palindrome, you just compare hash of string with it's reverse, for that substring.
That is not correct, you can do it for center of string, otherwise function is not monotonic and you can not use binary search:
Just look at string aba, there is two palindromes and binary search will check first ba and say, ok it is not palindrome answer is smaller than 2.
oh ok.. missed it :(
1:1 in hacks, we are playing until 2 ;)
It is easier to explain by considering only palindromes centered at indicies (so, odd length), the idea is the same anyway. For each index i, ri will be the longest radius of a palindrome centered there (in other words, the amount of palindromes centered at index i). Directly from manacher, this takes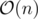 to calculate.
to calculate.
For a query [l, r], we first compute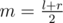 . Now we want to calculate
. Now we want to calculate
Again, thanks to symmetry, I'll only explain how to compute the left term.
The sum over i can be found in constant time. As for the other term, if we create some array ri' = ri - i during the preprocessing, then the queries are asking for some over range of min(C, ri') where C is constant. You can solve this in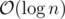 per query using wavelet tree, and I guess it's also solvable with a persistent segtree.
per query using wavelet tree, and I guess it's also solvable with a persistent segtree.
Thanks for your reply. This is an interesting approach.
Well, I am interested to know about this idea- min(i-l+1,r[i])=i+min(1-l,r[i]-i).
I have brute forced for different i,l and r[i] and found that this is true. But curious mind wants to know the proof of this. If you can come up with a proof feel free to share this with me.
Thanks again.
min(i - l + 1, ri) = min(i + (1 - l), i + (ri - i)) = i + min(1 - l, ri - i)
min(x + a, y + a) = a + min(x, y). I think this is fairly obvious, but you can do case analysis anyway:
Now just plug a = i, x = 1 - l, y = ri - i
thanks. got it
Palindrome tree can tall you, how many palindrome add s[i]. You can create partial sum array and say on query O(1).
Sorry for my English.
Please provide problem link.I want to solve it.
Happy solving
My approach takes O(n ^ 2) precalculation to get O(1) queries.
Can I improve furthur more with dynamic programming ?