Hi everyone,
Today I came across with this problem :
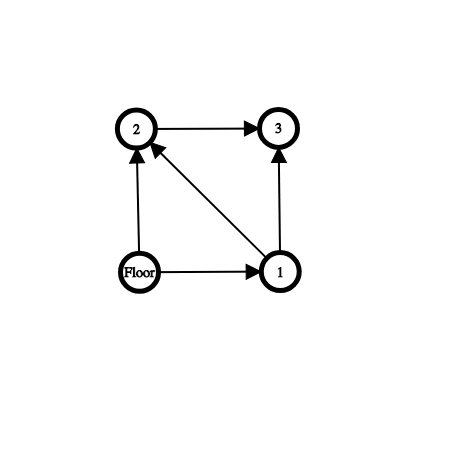
There is a rabbit on the floor of the stairs. Stairs have 3 steps, Rabbit can jump 1 or 2 steps. What is the probability of going to third step from the floor without visiting second step ?
Yeah I know its very easy to see there are 3 possible ways to go to 3 from the floor :
- floor -> 1 -> 2 -> 3
- floor -> 1 -> 3 ( This is the case we want).
- floor -> 2 -> 3
So the answer must be 
 .
.
Ok everything seems right. But if we represent this problem as a graph , In first step we must choose between 1 or 2 so the probability to go 1 is equal to 
 . In second step we must choose between 2 or 3 so the probability to go 3 is equal to
. In second step we must choose between 2 or 3 so the probability to go 3 is equal to 
 . So the overall the probability is equal to
. So the overall the probability is equal to 
 . Second solution have some differences from the first solution but I couldn't figure out what it is.
. Second solution have some differences from the first solution but I couldn't figure out what it is.










That's because the probabilities for cases 1, 2 and 3 aren't necessarily equal. Look at case 3. You can notice that the probability is actually 1/2 and not 1/3. Cases 1 and 2 are symmetric so both will have 1/4 probability.
I think eKKreamy's comment seems true. If you think that is wrong. Can you please explain ?
Imagine at a given moment you are at 2. Is there a difference between jumping 1 step or 2 steps?
No. So the probability to get from 2 to 3 with visiting 2 is 1.
Obviously the probability to get from 3 to 3 with visiting 2 is 0.
Now imagine we are at 1. The probability to get to 3 with visiting 2 is (1/2 * (probability from 2 to 3) + 1/2 * (probability from 3 to 3)) = 1/2 * 1 + 1/2 * 0 = 1/2.
Finally let's look at the moment when we are at the floor. We have 2 options. Go to 1 or go to 2.
Then the probability to visit 2 will be 1/2 * (probability from 1 to 3) + 1/2 * (probability from 2 to 3). This means that this probability is 1/2 * 1/2 + 1/2 * 1 = 3/4.
Then the probability to not visit 2 is 1 — 3/4 = 1/4.
Then the probability to visit 2 will be (probability from 1 to 3) +
(probability from 1 to 3) +  (probability from 2 to 3). You are wrong in this sentence because the first and second steps are not identical. Rabbit can go to the second step from the first step but it cannot do the reverse action of this action so this is why the probability of going to first step in the first jump is not
(probability from 2 to 3). You are wrong in this sentence because the first and second steps are not identical. Rabbit can go to the second step from the first step but it cannot do the reverse action of this action so this is why the probability of going to first step in the first jump is not  it is
it is  .
.
That's not how probabilities work.
floor -> 1 -> 2 -> 3 floor -> 1 -> 3 ( This is the case we want). floor -> 2 -> 3
I still think that , because of this. We choose one of this options so choosing the first step in the first jump is
, because of this. We choose one of this options so choosing the first step in the first jump is 
 as you can see.
as you can see.
Your problem is not properly defined. What does the rabbit randomly choose? The path or the next step?
Considering the rabbit randomly chooses the next step from the current step, your second solution is correct. In your first solution, the probability distribution of the 3 paths is not the same. You cannot directly say 1/3 by choosing 1 out of the 3 paths.
Experimental probability is the true solution to this problem. Calculating the probability via experiment: We have 3 options for going the third step from the floor. So we have 3 probabilities for the first jump. Two of them are the first step, one of them is the second step. We do not want to go to the second step so going the first step at the first jump has a probability of . Using the same method, the second jump must be the third step which has a probability of
. Using the same method, the second jump must be the third step which has a probability of  . Multiplying this two jumps gives us the answer
. Multiplying this two jumps gives us the answer  .
.
Yeah your idea seems right.
No, just because you have three possible outcomes doesn't mean each has probability one in three (aka the probability of winning the lottery is not one in two just because you either win it or you don't). In this case, in 2 you have only one option and will always go to 3. In 0 and 1 you can make two choices, I'm assuming that we select one uniformly. So the first two sequences above have probability , and the third one probability
, and the third one probability  . So the answer is
. So the answer is  .
.
EDIT: Going to repeat this and bold it because apparently not everyone in this thread gets this (-:
Second step and the first step are dependent so that's why we cannot say that going to the first step in the first jump is not .
.
TahsinEnesKuru I think we can relate it to the problem of finding the probability of reaching a particular leaf in a tree from the root. According to your first idea it should be 1 / (total leaves), hence all leaves are equiprobable, but it is wrong.