Traditionally, SnarkNews runs two New Year Contests.
The New Year Blitz Contest (Multiple Language Round) will start at 18:00 31.12.2018 and ends at 06:00 01.01.2019 Moscow Time. Contest consists of 12 problems. Some of those problems are based on problems, used at official or training contests in 2018. Contest rules are based on the ICPC system with two important modifications.
Penalty time is calculated as distance between time of first successful submit for the contestant on this problem and 0:00:00 01.01.2019, i.e. successful submissions at 23:50:00 31.12.2018 and at 0:10:00 01.01.2019 will both have penalty time 10 minutes (600 seconds).
Multiple Language Round rule: If for the first successful submit for the contestant on the some problem was used the programming language, which was never used by this contestant in his previous first successful submits on other problems, contestant receives language bonus: his summary penalty time is decreased by 100 minutes (6000 seconds). Note that different implementations of the same language are counting as same language, i.e. Java 6 and Java 7 are both counted as Java, C++ 32 bit and C++11 64 bit both as C++. Additionally, C and C++ are counted as same programming language.
Contest will be running on Yandex.Contest system. Link for registration and participation.
15'th Prime New Year Contest will start at 03:00 30.12.2018 and finish at 15:00 23.01.2019 Moscow time. Traditionally, Prime New Year Contest consists of problems, which were presented at team programming contests in 2018 and never solved on the contest. Because for 2018 list of those problems is big, the contest time is doubled compared to previous years. For the Prime New Year contest plain ICPC rules are used.
Idea of Prime Contest was first implemented by Andrey Lopatin and Nick Dourov at Summer Petrozavodsk training camp at 2003; in Russian word "Prostoj" used in meanings "prime" and "easy", so, contest was called "Prostoj contest" but was composed of extremelly hard problems, numbered with prime numbers (2,3,5 etc). Since then such a numeration is traditionally used for contests, consisting of very hard problems only.
Contest will be running on Yandex.Contest system. Link for registration and participation.
Both contests have English statements. Registration is open till the end of the contest.











There is an option to register as a team but I cannot find the option to create a team. Is it even possible to compete as a team?
I always think that Prime New Year Contest should have more participants, so here is a friendly bump for those who may have not seen this blog before.
The timing is bad. Most people have exams during this time. Usually it only affects the first exam in January, but this year it got extended by 2 weeks and it's much harder to participate now.
Huh, unfortunate. In Poland we have exams at the end of January and beginning of February, so beginning of every year is pretty calm unless you have close deadlines for some big programming projects. Or you can be too old for exams like me xd. However, on the bright side, Prime Contest was extended by ~2 weeks as well :P.
I wanted to, but I'm trapped in translation hell. Btw, I can use this as an ad for a physics competition for secondary school students (even international, with some restrictions), which runs onsite in 28 days and is horribly behind schedule right now.
kriii and ko_osaga are very curious over the solution of 101, especially the one that does not involve sqrt.
Let's maintain "almost centroid decomposition" for each component. When we add new edge between components we can merge them similarly to how we merge treaps: start with the roots, add all vertices from smaller component to the bigger one and go to a child of the root. Obviously, this solution is quadratic in time. To make it faster we need to rebuild centroid decomposition sometimes. Let's store for each vertex current size of its subtree (in decomposition tree) and also the size of its subtree at the last time it was rebuilt. If current size becomes 2 times larger, we need to rebuild the whole subtree from scratch. If we do this, then for each vertex in decomposition it is true that the size of its largest child subtree is not more than 3 / 4 of its own subtree, so the depth is still logarithmic. Overall solution works in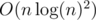 . Code.
. Code.
That's basically the same way I and mnbvmar solved this as well with a slight difference that we rebuild a subtree of some centroid when it turns out to be highly unbalanced which means some of its son's subtrees is bigger than 3/4 of size of this vertex subtree. Same complexity though, obviously.
OK, so the time has come. I spent a freaking amount of time on this contest (rough estimate should be 70 hours), just as I do every year, but number of problems this year was enormous and what is more I got a feeling like an average problem is harder than average problem in previous years. Or maybe it is just me getting dumber and lazier. And now I can't wait to get to know solutions of problems I couldn't solve.
I'm particularly interested in solutions of 17, 19, 41, 43, 53, 59, 61 and 83. For remaining ones I didn't solve I believe I have a rough idea of how to solve 23, 47, 67, 89, but was too lazy to do code them/dig into details and 97 is just nah. If any of you aid sunset mnbvmar Radewoosh can shed some light on these problems, I would be grateful. If anybody is interested in how I solved some problem I can tell this as well.
17: Getting formula is trivial, just evaluating it on bigints is problem. Keep numerator as bigint and denominator in factorized form. Getting answer in possibly reducible fraction using D&C is easy, but assuring that gcd(p, q)=1 is the hard part. I think there should be not too many divisions required but testing whether nominator is divisible by something should be done in some smart way.
19: I am quite sure both parametric search and 2-matroid intersection are involved here, but couldn't get it in one piece.
43: Uh oh, I am kinda frustrated I didn't get this one since this had many ACs and I thought I am so close. I figured out that it is somewhat similar to counting in how many ways I can put k non-attacking rooks on triangular chessboard (consisting of cells (i, j) so that i <= j) and answer to that is some Stirling number and using some formula that is different than million formulas about Stirling numbers that I saw in the Internet I am able to compute them using inverse of generating function. However what I need to do in this task is count them on a triangular chessboard with one row removed and I couldn't handle that.
61: Parametric search + convex hull trick solves a version on a line, but I couldn't get the cycle right even though I got some ideas about random cutting the cycle when k is big or some D&C-ish thoughts.
67: Just to make sure, this is some combination of inverting and taking square root of a few generating fucntion together, right?
83: I saw this post from zemen https://codeforces.com/blog/entry/63449#comment-473698 and a followup by aid but even with its help I couldn't get this one right. First thing is that computing multiplicities of these pairs (chain(t), chain(bt)) was kinda costly. I think I can do it in reasonable preprocessing time of something like 20 mins, so that's doable but I believe there should be a better way. Even after doing that, I couldn't get how should I do the second part. Inclusion-exclusion seemed like a good way to go, but there were too many things that we need to keep track of and I got lost.
Btw when I was bored I created "standings" of problems which I have solved according to a few criterions:
Ugliness of code: 13 < 11 < 5 < 71 < 29 < 37 < 3 < 79 < 7 < 101 < 31 < 2 < 73
Difficulty of coming up with a solution: 79 < 29 < 11 < 37 < 7 < 2 < 73 < 101 < 71 < 3 < 31 < 13 < 5
How fun the solution is: 79 < 73 < 37 < 29 < 2 < 11 < 7 < 101 < 71 < 31 < 3 < 5 < 13
If I were to add 89 to this which I came up with a solution at 5 AM today it would be very close to top in all these 3 charts.
17: Let k be the number of unreasonable shops, x be their average price and y be the average price of reasonable shops. Then the answer is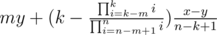 (there are some corner cases when k = 0 or k = n or m ≥ k but they are easy). First we calculate
(there are some corner cases when k = 0 or k = n or m ≥ k but they are easy). First we calculate 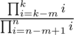 . We can factorize each i and delete all primes that appear in both numerator and denominator. After that we calculate numerator and denominator with divide and conquer. Now we have irreducible fraction
. We can factorize each i and delete all primes that appear in both numerator and denominator. After that we calculate numerator and denominator with divide and conquer. Now we have irreducible fraction  . To get our formula from it we only need 3 operations:
. To get our formula from it we only need 3 operations:
1) Add a small integer a to . We replace p with p + aq. After that fraction remains irreducible.
. We replace p with p + aq. After that fraction remains irreducible.
2) Multilpy by a small integer a. We compute
by a small integer a. We compute 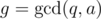 (we only need to find
(we only need to find 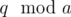 , after that it's just gcd of 2 small numbers). Then we divide both a and q by g and multiply p by a.
, after that it's just gcd of 2 small numbers). Then we divide both a and q by g and multiply p by a.
3) Divide by a small integer a. This is the same as 2).
by a small integer a. This is the same as 2).
Overall the only operations we need are addition and multiplication of big integers, and division and taking modulo of a big integer by a small integer.
19 is just matroid intersection. What's the problem?
The problem is that there is some weird weighted version with dijkstra instead of bfs, which as I know doesn't actually work in general case? And I have no understanding why does it work in this problem.
I am sorry but this is not "just matroid intersection, what's the problem?" for me :). Care to elaborate more on that? Is there really no parametric search involved (adding +c to green edges for some constant c) at any point? Is there any linear algebra/Gauss elimination involved (since linear represantations are often used when dealing with matroids)?
I am the author of 2 and 3, and I was almost sure that nobody would write 2 in a Prime contest, there are a lot of other problems (there were some people during PTZ, and I feel little sorry for them, but PTZ camp is a special place). Good that I was wrong, and you've got as much joy and fun as did I during the preparation of the problem! Also, there was a 14-hour stream of 300iq solving this problem :)
Yeah, it was kinda nightmarish to code, I used segment tree with 13 attributes in each node, but at the same time it was pretty easy to come up with a solution and it's New Year Prime contest — you can't simply turn away problem since it is tedious to code because otherwise you are left with 2 problems to solve xD. By the way since I participate (this was my fourth time), all problems were solved, so nobody solving some problem would be kinda huge. During Prime contest I have much more determination and free time than I ever have on any camp as well ;p.
Btw I really liked problem 3, but I think when posing it on PTZ contest you could have shown at least some mercy and not require restoring answer :p. Btw not sure if everybody realizes, but perfect elimination order can be quite simply computed in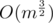 using triangle counting. Never got to learn LexBFS, so I don't now if it actually turns out to be significantly simpler, but at least it is possible to come up with it by yourself and for lexbfs I guess it is not?
using triangle counting. Never got to learn LexBFS, so I don't now if it actually turns out to be significantly simpler, but at least it is possible to come up with it by yourself and for lexbfs I guess it is not?
PEO can be easily computed in linear time (actually with logarithm to get the easier code) by MCT (maximal cardinality search): on each iteration just take the vertex, which is connected to the maximal number of already taken vertices. This algorithm also constructs the Clique tree, which I use to do a dynamic programming in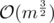 .
.
I wasn't able to debug my solution without printing the certificate, so I've decided to help participants with debugging solution — with restoring the answer it is much easier to see where you are wrong :)
Haha, my dp was working fine before printing the certificate and mnbvmar used other nondp approach with some tricky contracting edges leading to introducing weights etc (I came up with it for outerplanar graphs, but couldn't generalize it to any chordal graph, so I went for dp) and restoring answer from that must have been a real pain.
And a really nice algorithm for PEO! I see that key idea is to do it in reverse manner.
I don't think that 2 is that difficult to code. Of course, I wouldn't try to write it during the contest, but it's not even close to 97 or 89. If you think about it carefully, the solution will not look that scary. I stored 2 treaps: one for segments of time, during which the guards are to the right of current edge and the other for segments of time when they are to the left. When we go from one edge to the next, we delete some segments, add some new ones and shrink all existing ones(in the second treap we extend them instead of shrinking but it's the same). Shrinking segment [l, r] by x transforms it into segment [l + x, r - x]. It is easy to do it with lazy propagation. We also need to answer the query: what's the leftest segment with length at least t? It is also easily done with maintaining maximal length of segment in the subtree. Here's the code. It's pretty long, but all parts are easy by themselves, there's just a lot to write.
43 can be solved for any Young diagram. Look at falling factorial generating function: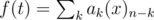 , where ak is number of ways to place k rooks on a board. My solution is
, where ak is number of ways to place k rooks on a board. My solution is 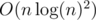 , but I think there should be some faster solution, because I had to optimise it heavily and it still works in 2.5 seconds.
, but I think there should be some faster solution, because I had to optimise it heavily and it still works in 2.5 seconds.
A rough idea of my approach to 43: as above, we notice that placing bishops on each chessboard color is equivalent to placing rooks on a Young diagram. If such a diagram was triangular:
then the number of ways to place k rooks would be described by Stirling numbers of the second kind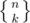 . We would need to compute a generating function of the form
. We would need to compute a generating function of the form 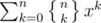 . Such a generating function exists, and is of the form e - x·(some pretty generating function).
. Such a generating function exists, and is of the form e - x·(some pretty generating function).
In our case, the diagram is a bit different, something like this:
However, it still turns out that the equivalent generating function is still of the form e - x·(something pretty). I'm omitting quite a few technical issues here but each term of that "pretty" generating function can be computed independently, and done easily in time. Therefore, we can compute the "whole" generating function in
time. Therefore, we can compute the "whole" generating function in  time. AC'd in 0.4s/3s.
time. AC'd in 0.4s/3s.
53: There is an obvious way to transform one tree into another one: contract all edges and then grow new ones. But in the optimal way some edges are relabeled instead of contracing and then regrowing them. We need to choose some pairs of edges that should be relabeled so that the cost is minimised. Of course there are some restricions. For example, if edge e1 was inside the subtree of edge e2 in the first tree then they should stay the same way in the second tree. To formalise this let's build a bracket sequence: go through all edges in dfs order and when we go down edge e append (e to the sequence and when we go up edge e append )e. Let the bracket sequences for both tree be s1 and s2. If we want to transform edges e1, ..., ek in the first tree into edges e'1, ..., e'k in the second tree, then the corresponding bracket subsequences in s1 and s2 should be isomorphic. Now we have a solution: do a substring dp: dpl1, r1, l2, r2 is the minimal cost to transform some edges with both brackets in segment [l1, r1] of s1 into edges with both brackets in segment [l2, r2] of s2. This solution is too slow, but when you think how dp is calculated you can notice that we can only use segments in s2 where s2[l2] = (e and s2[r2] = )e. In other words, we can do this dp: dpl1, r1, v2 is the minimal cost to transform some edges in segment [l1, r1] of s1 into edges in the subtree of v2 in the second tree. This dp is calculated in O(nm3), where n and m are the size of trees. The code is very simple.
Btw what I find surprising about this problem is that it is symmetrical in a way that answer stays the same if we swap trees and swap c1 and c2, but solution breaks this symmetry.
Another approach: dp[l1][r1][l2][r2]: match [l1, r1] in tree1 and [l2, r2] in tree2. Contract: trans from dp[l1+1][r1][l2][r2] or dp[l1][r1-1][l2][r2] Otherwise, we can trans from either l2 or r2. Choose the one with smaller subtree size. O(n^2mlog m).
Regarding 83, there are a lot of chains that have no strings corresponding to them. To find them count multiplicity of each chain when k = 40. If you delete all of them, there will be only about a thousand chains for strings of length 40. When we count multiplicity of pair of chains we need to subtract multiplicities of its superchains. So we also calculate all superchains for each chain. Then we do the same optimisation with pairs of chains: find their multiplicities when k = 40, if it's 0, when delete this pair. After that number of pairs of chains is just about 8000.
The second part is done with some ugly dp. Parameters are length of string, is t prefix of our string, is t suffix of our string, or something like that.
I wrote an editorial. Hope it explains better.
61: First let's solve the problem on a line instead of a circle. Easy to solve it in O(nklogn). Use the trick from IOI 2016 "aliens" then the problem can be solved in O(nlognlogV).
Let's get back to the original problem. Let the best answer of the problem be p[1...k], and the best answer start from q[1] be q[1...k]. Assume that p[1]<=q[1]<=p[2], it's easy to see p[i]<=q[i]<=p[i+1](quadrangle inequality). Let q[1]=0, and we find q, find i which minimizes q[i+1]-q[i]: it's not greater than n/k. Then try to use divide and conquer to find the best p[i].
UPD: I didn't notice Radewoosh had already posted the solution. It's correct and here is my implemention: https://ideone.com/mE7QKW
59: It's trivial to solve the problem in O(nm) time(there is at most one path start from one vertex).
If we can find a Hamilton cycle in the graph, it's also easy to solve this.
Let in[i] be the in degree of i and out[i] be the out degree of i. If in[i]>=2 and out[i]==1: i won't be the end point and the next point of i can be determined. Now if in[i]==0 or out[i]==0 for some i, there's only one solution. Now in[i]==1&&out[i]==1(type A) or out[i]>=2(type B) always holds. If there's no type B vertexes: the graph has a Hamilton cycle or it's not connected. Otherwise, we can only start from type A vertexes.
For each type A vertexes, the path start from it looks like: A1->A2->A3->A4...->Ak->B1->..., there exists an edge B1->A1. We can see there are at most two such paths exist(once we go from B1 to A1, we'll end at Ak).
13 is one of my favourite problems ever. My head exploded several times when I tried to solve it, but the final solution turned out to be so simple.
83 is very cool, but I solved it before the contest.
29 is also nice although a bit standard. When I read the statement I was surprised that it's solvable.
Surprised that so few people solved 53 and even more surprised that such an easy problem was not solved in GP of Zhejang. I think it was the second easiest problem there. I guess the statement looks scary: it feels like there will be a lot of casework and solution should be very hard. At least that's what I thought and because of that I solved other problems instead. When I actually tried to solve it a few days ago I couldn't believe that it has such a simple solution.
Also surprised that problems 11, 17 and 19 ended up in this contest. They are pretty obvious and easy to implement. Especially 19 which is just a standard algorithm without any other ideas.
37 looks like a marathon problem. Is there an cool way to solve it(not simulated annealing/genetic algorithm/etc)? If not then what's the point of giving it on ACM contest?
Regarding 37, I was surprised how easy it turned out to be. You need a few basic ideas:
1) Have you even solved a "fifteen puzzle"? I guess so and you should take a lesson from it that board should be filled in some reasonable order, e.g. row major order or I used a bit more fancy comparator which is max metric from last cell:
2) Prefer using smaller pieces only when it's a necessity cause smaller pieces are useful the most when you have not a lot of freedom == at the end of process.
3) Keep uncovered cells connected since you won't succeed if you create some area with 1 or 2 uncovered cells blocked from the outside world.
4) Restart from scratch if not successful.
So I basically go through all cells in order I explained and if a cell is not covered yet I try putting there random tile in random rotation preferring bigger ones caring to not disconnect uncovered cells. That's it.
At the beginning I thought that I should do some backtrack at the end, but just for fun midway through coding process I decided to check how my current version without backtrack runs and I was really surprised to see that it actually fully solves the problem. In my code you can spot an empty section with comment "start bt" xD.
My code is here: https://ideone.com/5omSlx
Regarding 13, I agree with you. It was really great problem and indeed after reading it I classified it to "brain explosion" category. Glad to see that you described it in the same way :D.
Regarding 11, I agree as well. Both me and mnbvmar were like "what? this is completely trivial, contestants must have been drunk this day" :P
Regarding 19 — "They are pretty obvious and easy to implement. Especially 19 which is just a standard algorithm without any other ideas." — wot de fook man XD. Both me and Marek were like "omg, this is some completely crazy stuff, what kind of a madman would put matroids and parametric search together on a contest?", and you're like "especially 19 which is completely standard without any other ideas" xD
Regarding 53 I felt the same way, that it should be very easy, but I somehow got lost in what should I keep track of.
For problem 37, what you describe is similar to my solution, and yeah, I had backtracking there, instead of the "restart from scratch" item. However, in a contest, under time pressure, throwing in a simple "restart from scratch" heuristic is of course more likely than writing a full backtracking implementation on top of a load of existing code.
As to why include such problem in an ICPC problemset, there are several reasons.
Simple: it's a "true story" problem, I had my daughter Dasha solve a real world version, smaller and easier of course. I then became genuinely interested in how to do it in the general case.
Most contestants just can't solve some problems completely in their heads, and require tools. Usually, these tools are pen and paper. In a team contest, discussing with a teammate is a powerful tool. Sometimes a computer is used in the solving process to write a simple program, produce some outputs (e.g., Grundy numbers, or some other table for small inputs), print and stare at them until an idea comes to mind. I just happen to like the problems where the most helpful tool is the computer itself, when you have to try to implement various hypotheses just to see what works and what doesn't. In a team contest where computer time is scarce, this calls for interesting decisions and tradeoffs.
In the particular contest, I had 31 and 37 as hard problems, so that no team was expected to solve everything, but the top teams likely had a choice of what to solve. Unfortunately, the difficulty was a bit overwhelming, so both problems ended up here (and being solved in upsolving).
31 was kinda fun to come up with solution, but a nightmare to code, much much harder than 37 even considering implementation only. And bignums to top that off.
Tbh, I'm not sure, what is code of honour for Russian teams on camps/opencups? Is copying codes allowed? We never copied anything on Ptz or even regular team trainings, we were rewriting our paper library when needed.
As far as I know, there's usually no strict enforcement of such rule, but copying is generally discouraged. The number one reason is that camps are primarily training for ICPC World Finals and semifinals, so to make the most out of it, the contestants should follow the rules of these contests as closely as possible.
On OpenCup copying is allowed (though I think that most teams that are training for WF don't use it).
Surprised that you liked my problem (29), but a lot more surprised to see it in Prime Contest. It is weird how snarknews chooses problems for it. I thought problems from training camps which were solved in upsolving (by someone who is not the author) shouldn't get there. I just checked: two problems from our 2016 Ptz contest which also weren't solved in 5 hours were not in Prime Contest despite (in my opinion) being harder and much more interesting.
About 53: Well, I guess all the participants were just overwhelmed with the hardness of the contest. Our team didn't even managed to get the only easy problem in first 2 hours. It is easy to miss one problem among 11.
About 19: Maybe you will write some tutorial about matroids? I don't know a thing except like "matroids is a thing and you can prove some greedy algorithms but why would you bother on a contest".
About 37: The answer is "this is a problem by Gassa". I don't see a point either.
"About 37: The answer is "this is a problem by Gassa". I don't see a point either." — that's your daily Um_nik at its best xD
And regarding 29 and its presence. I thought that in previous years problems from Ptz were not included at all (sure about Ptz 2016 and Ptz 2017 where I was), only OpenCup GPs or some regional stages were considered I believe. And in this year there were a lot of them. However I may be a little off, I think I recall seeing some problems (beautiful one about binary search in log n + 0.1 instead of ceiling(log n) and some tedious path selection which I coded for 7 hours straight) which were from some other camp than Ptz, I believe. Rules for choosing problems are not clear to me, I guess it just depends on snark's mood. And yeah, I think this was the easiest problem next to 11, it was rather straightforward to me how to solve it and it wasn't that hard to code it as well, however I fell into a few traps when coding it (graph disconnecting after reductions where more than one cycle could have appeared etc), so in the end it took me much more time than I expected.
Well, Gassa is the only problemsetter I know who on regular basis giving problems like "Write some bruteforce with breaks. I spend a week optimizing it so now my solution works under 10 seconds, so now it is OK to give it to the contest" or "Here is a real text of War and Peace. Do something using that it is a real text and also do not forget to do something about it containing names of the heroes which are not real English words. Oh, and also there are some letters in English which are rarely used and it will fuck up some statistical approaches but not other because reasons". I don't like it but I think that Ptz is one of the few places where such problems are acceptable, because there we can widen our concepts about what can and cannot be an algorithmic problem.
Regarding tutorial on matroids, I think this is a good source: http://parameterized-algorithms.mimuw.edu.pl/parameterized-algorithms.pdf It is a really great book with a lots of awesome and accessible stuff. Matroids are in Chapter 12. However it wasn't sufficient to me to solve 19 xD.
OK, I will try to write a tutorial when I will have free time.
37:
Consider cells in this order:
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 65 69 73 77 81 85 89 93 97
62 66 70 74 78 82 86 90 94 98
63 67 71 75 79 83 87 91 95 99
64 68 72 76 80 84 88 92 96 100
and use backtracking. Prefer using larger polynominos firstly. After 104 calls of the recursive function kill it and restart with shuffled polynominos. Cut every time when there is a single surrounded cell (or pair of cells).
41:
Well, I managed to solve it with a time-heuristic. It's obvious that this task can be solved brutally by building a suffix automaton and for each node calculating vector of bits. So, I've replaced this vector of bits with a persistent treap. The operations that I have to do are: flip every value in some treap (so there will be a lazy propagation) and calculate OR value of two treaps. I do the second operation as follows: If one of the treaps contain only zeroes — return the second one. If one of the treaps contain only ones — return it. If two sequences of bits are identical (so I calculate hashes for treaps) — return any of them. If two treaps would match perfectly (for example both of them contain alternating zeroes and ones with different parity) — return preprocessed treap with ones. If no condition is met -- split both of them and calculate OR recursively. This makes a lot of sense if you know how these arrays of bits look like (most of them look like 000000000000001010101 or 11111111111101010101, but no, this isn't a rule).
61 (not solved on the contest, but I think that it's correct):
Firstly -- solve it on a line, not on the circle. It can be done with parametric search (to get rid of the second dimension of dp) and two convex hulls (one of them for villages which have the closest post office to the right and one of them for the rest). These convex hulls are used alternately.
Now comes the hardest part of the task: we have to fix any beginning, calculate the result for a line version and restore the answer. Look at the positions of the borders of intervals in our line-solution. By interval I mean the interval of villages which go to the same post office and the border is... you know, the space between two intervals. In optimal solutions, there will be exactly one border of intervals between every two neighboring borders from the line-solution, and maybe it will be one of these borders from line-solution (and maybe not).
Sanity check: if we know the beginning and the end of some interval, we know where should we build a post office — in the middle (median things).
Now the whole sequence is partitioned into k fragments, and we know that each of them will contain exactly one border. In a brutal solution, we would just iterate over the position of the border in the first fragment and run some dp. But we want to do it faster. Fix a position of the border in the first fragment in the middle of it and run dp. Restore the answer. Now we know, that if we'd move the border in the first fragment to the right, the optimal borders in other fragments won't move left (it can only move to the right or not change). Same with moving to the left. So we do something similar to the d&c trick. We split each of the k fragments into two smaller ones (and first of them is split into two halves, so the deep of the recurrence will be O(log(n))) and run recursively. The sum of the lengths of the intervals in each level of the recursion is equal to n + k·(number of calls of the function on this level). To make this value not greater than 2n, we can choose the smallest fragment as the first one, it isn't longer than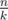 .
.
Last thing is how to do the transitions from one fragment to the next one faster than O(product of the lengths). Just d&c trick.
Regading 41 actually I have no idea how to determine if some substring is winning or not in an (almost) linear time. If we were just adding letters to back this would be simple dp on suffix automaton which I learnt for a purpose of solving 83, but unfortunately I do not see what is going on when we are appending letters to front of it as well. Probably dp on product of suffix automaton and suffix automaton of reversed string would do the thing for a polynomial solution, but I don't think this should be a way to go.
Intended solution is actually O(n) and supposes building a symmetric compacted suffix automaton.
Brief sketch of the solution:
Both suffix automaton and suffix tree imply some equivalence relations by their vertices.
Namely, consider vertex v in suffix tree and all strings in suffix tree which end on the edge from v to its parent (including string for v and excluding string for the parent of v). Let's define left context [x]L of string x as largest string xα such that x always come with α when it occurs in the string. Then all strings on the edge of v have same left context, which is exactly string which ends in v.
Similar is true for suffix automaton, but with right context [x]R, which is largest string β x such that x is always preceded with β when it occurs in the string. So, there is one to one correspondence between right context and nodes of suffix automaton for given string.
Now let's define context [x] = [[x]L]R = [[x]R]L which is largest string β xα such that x is always preceded by β and succeeded by α when it occurs in the string. Turns out that there is one to one correspondence between context of the string and nodes in compacted suffix automaton, which is what we get if get rid of states with out-degree 1 in regular suffix automaton, or if we minimize the suffix tree considering its edges to be characters of some alphabet Σ.
Now those contexts have some peculiar properties.
Given all that it's possible to construct the final solution, but there are lot of technicalities...
P.S. Maybe I will write some comprehensive article on compacted automatons one day, they're pretty cool :)
So, why didn't you share your solution for 41 with me when I asked? :(
(P.S. for all the others: I'm the author of the problem)
for suffix automaton, but with right context [x]R, which is largest string β x such that x is always preceded with β when it occurs in the string. So, does it mean β can be empty ?
For 41, what's the meaning of vector of bits?
89: at a first glance, the problem looks like "whaaaat why would anyone torture us with such a problem, Goooood whyyyyy please take this from me". It turns out to be really exciting in the end.
How to think about 89: we have two machines being able to communicate with each other. Each of them can send at most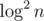 bits of information. The first of them knows some clique, and the other knows some independent set in a known graph. They need to decide if these two sets intersect. (Obviously, the intersection can't be larger than one vertex.)
bits of information. The first of them knows some clique, and the other knows some independent set in a known graph. They need to decide if these two sets intersect. (Obviously, the intersection can't be larger than one vertex.)
Note: this would probably make a great IOI-style problem assuming such communication is technically viable in IOI setting. I hope the setters tried submitting the problem to the IOI committee before proposing it to the OpenCup.
How to solve 89 in this setting: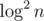 bits usually means
bits usually means  vertex IDs (each of them is a
vertex IDs (each of them is a 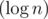 -bit number). We'll therefore have
-bit number). We'll therefore have  rounds of communication. In each of them, the clique machine will submit one of the vertices belonging to the clique, and the independent set machine will submit one of the vertices belonging to its own set.
rounds of communication. In each of them, the clique machine will submit one of the vertices belonging to the clique, and the independent set machine will submit one of the vertices belonging to its own set.
After each round, each machine knows some subset of vertices belonging to the clique and a subset of vertices belonging to the independent set. If there is an intersection x between the clique and the independent set, and x belongs to one of the submitted subsets, both machines can realize that in a single round and return success. If x doesn't belong to any of these subsets, it must be connected to all the vertices submitted by the clique machine and to none of the vertices submitted by the independent set machine. We can therefore shrink the graph by dropping the vertices not fulfilling these properties. If no clique/independent set vertices remain in such a graph, we declare the failure. Note that the constructed subgraph is the same in both machines.
We now aim to drop the number of vertices in the graph by a factor of 2 in each round. How to do it? The clique machine takes the subgraph and locates the vertex vC with minimum degree belonging to the clique. The independent set machine takes the subgraph and locates the vertex vI with maximum degree belonging to the independent set. Now, if there is a non-empty intersection {x} of these sets, then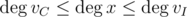 . Then:
. Then:
Therefore, if there exists a solution, we will succeed in rounds. If this is not the case, we simply declare the failure after
rounds. If this is not the case, we simply declare the failure after  steps.
steps.
How to translate the solution into circuits: well, here comes the not-overly-exciting part. There are still some complications as I needed the size of the circuits to be asymptotically lower than n2 which is pretty tricky in a couple of spots:
97:
There's probably not much more to add to this. Just simulate what they say, only that you need to do it freaking efficiently and be able to rollback the operations (to see which possible move is the best). After some debugging hell, you still need to optimize your solution tenfold to pass. Can someone make up for my sleepless night? :<
AFAIK, you should use some data structures to speed up the process of falling down. Otherwise the time complexity is wrong.
Okay, if there is a good selection of data structures allowing us to achieve constant time complexity per coin removal/reinsertion, I'd love to know it. The best I could achieve was per operation (with a simple segment tree) which actually behaved way worse than even slightly optimized O(n) XD. I feel intuitively why this happened, but it was strange nevertheless.
per operation (with a simple segment tree) which actually behaved way worse than even slightly optimized O(n) XD. I feel intuitively why this happened, but it was strange nevertheless.
Either way, I think that requiring the participants to write a bunch of ugly stuff (which I personally don't mind, and maybe even like in some masochistic way) and expecting them to strive for the best possible time complexity sounds quite bad.
My rule of the thumb is: if you have some nice algorithmic tricks in mind, you should probably drop all/majority of messy parts of the problem (and make it more accessible to contestants). If you simply want us to simulate a complex game, don't push for high constraints.
Btw, solution for #71 is one of the coolest thing I've learned last year. I hope it could be known for more general audience, because the fact that incremental SCC could be done in very clean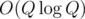 D&C is just so fucking awesome. Solution sketch by toosimple
D&C is just so fucking awesome. Solution sketch by toosimple
It would be nice if I was able to devote more time in this contest (unsolvable problems are always cool), but I spent most of time doing IOI winter camp tutor, and for the rest of time I was quite tired with sqeezing my sqrt in #101 :(